
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象相交于点A(-2,1),B(1,n).
的图象相交于点A(-2,1),B(1,n).
(1)求此一次函数和反比例函数的解析式;
(2)在平面直角坐标系的第二象限内边长为1的正方形EFDG的边均平行于坐标轴,若点E的坐标为(-a,a),当曲线y=![]() (x<0)与此正方形的边有交点时,求a的取值范围.
(x<0)与此正方形的边有交点时,求a的取值范围.

【答案】(1)反比例函数的解析式为y=-![]() ,一次函数的解析式为y=-x-1;(2)a的取值范围为
,一次函数的解析式为y=-x-1;(2)a的取值范围为![]() ≤a≤
≤a≤![]() +1.
+1.
【解析】(1)∵点A(﹣2,1)在反比例函数y=![]() 的图象上,
的图象上,
∴m=﹣2×1=﹣2,
∴反比例函数解析式为y=﹣![]() ;
;
∵点B(1,n)在反比例函数y=﹣![]() 的图象上,
的图象上,
∴﹣2=n,即点B的坐标为(1,﹣2).
将点A(﹣2,1)、点B(1,﹣2)代入y=kx+b中得:
![]() ,解得:
,解得:![]() ,
,
∴一次函数的解析式为y=﹣x﹣1 .
(2)不等式﹣x﹣1﹣(﹣![]() )<0可变形为:﹣x﹣1<﹣
)<0可变形为:﹣x﹣1<﹣![]() ,
,
观察两函数图象,发现:
当﹣2<x<0或x>1时,一次函数图象在反比例图象下方,
∴满足不等式kx+b﹣![]() <0的解集为﹣2<x<0或x>1.
<0的解集为﹣2<x<0或x>1.
(3)过点O、E作直线OE,如图所示.

∵点E的坐标为(﹣a,a),
∴直线OE的解析式为y=﹣x.
∵四边形EFDG是边长为1的正方形,且各边均平行于坐标轴,
∴点D的坐标为(﹣a+1,a﹣1),
∵a﹣1=﹣(﹣a+1),
∴点D在直线OE上.
将y=﹣x代入y=﹣![]() (x<0)得:
(x<0)得:
﹣x=﹣![]() ,即x2=2,解得:x=﹣
,即x2=2,解得:x=﹣![]() ,或x=
,或x=![]() (舍去).
(舍去).
∵曲线y=﹣![]() (x<0)与此正方形的边有交点,
(x<0)与此正方形的边有交点,
∴﹣a≤﹣![]() ≤﹣a+1,解得:
≤﹣a+1,解得:![]() ≤a≤
≤a≤![]() +1.
+1.
故当曲线y=![]() (x<0)与此正方形的边有交点时,
(x<0)与此正方形的边有交点时,
a的取值范围为![]() ≤a≤
≤a≤![]() +1. /span>
+1. /span>


科目:初中数学 来源: 题型:
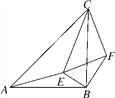
【题目】如图,△ABC和△CEF均为等腰直角三角形,E在△ABC内,∠CAE+∠CBE=90°,连接BF.
(1)求证:△CAE∽△CBF;
(2)若BE=1,AE=2,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y=![]() .
.
(1)若该反比例函数的图象与直线y=kx+4(k≠0)只有一个公共点,求k的值;
(2)如图,反比例函数y=![]() (1≤x≤4)的图象记为曲线C1,将C1向左平移2个单位长度,得曲线C2,请在图中画出C2,并直接写出C1平移到C2处所扫过的面积.
(1≤x≤4)的图象记为曲线C1,将C1向左平移2个单位长度,得曲线C2,请在图中画出C2,并直接写出C1平移到C2处所扫过的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【探究函数y=x+![]() 的图象与性质】
的图象与性质】
(1)函数y=x+![]() 的自变量x的取值范围是________;
的自变量x的取值范围是________;
(2)下列四个函数图象中,函数y=x+![]() 的图象大致是________;
的图象大致是________;

(3)对于函数y=x+![]() ,求当x>0时,y的取值范围.请将下列的求解过程补充完整.
,求当x>0时,y的取值范围.请将下列的求解过程补充完整.
解:∵x>0,∴y=x+![]() =(
=(![]() )2+
)2+![]() =
=![]() +________.
+________.
∵![]() ≥0,∴y≥________.
≥0,∴y≥________.
【拓展运用】
(4)若函数y=![]() ,求y的取值范围.
,求y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年10月17日,神州十一号飞船成功发射升空.发射当天约有161000个相关精彩栏目的热门视频在网络上热播.将数据161000用科学记数法表示为( )
A.1.61×103
B.0.161×105
C.1.61×105
D.16.1×104
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com