
分析 先求出这组数据的平均数,再根据方差公式进行计算即可.
解答 解:该运动员这五次成绩的平均数是:(181+177+181+182+179)÷5=180,
则方差=$\frac{1}{5}$[(181-180)2+(177-180)2+(181-180)2+(182-180)2+(179-180)2]=3.2.
故答案为3.2.
点评 此题考查了方差,用到的知识点是方差公式,一般地设n个数据,x1,x2,…xn的平均数为$\overline{x}$,则方差S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC在网格中(每格表示1个单位),如图所示构建平面直角坐标系
如图,△ABC在网格中(每格表示1个单位),如图所示构建平面直角坐标系查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
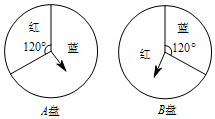 小明和小丽用如图所示的两个转盘做“配紫色”游戏:分别转动两个转盘,其中一个转盘转到红色,另一个转盘转到蓝色,即可配成紫色,两人商定,若能配成紫色,小明胜,否则小丽胜,这个游戏对双方公平吗?请说明理由.
小明和小丽用如图所示的两个转盘做“配紫色”游戏:分别转动两个转盘,其中一个转盘转到红色,另一个转盘转到蓝色,即可配成紫色,两人商定,若能配成紫色,小明胜,否则小丽胜,这个游戏对双方公平吗?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
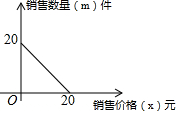 某商场以每件10元的价格购进一种商品,试销中发现,这种商品每天的销售量m(件)与每件的销售价x(元)满足一次函数,其函数图象如图所示.
某商场以每件10元的价格购进一种商品,试销中发现,这种商品每天的销售量m(件)与每件的销售价x(元)满足一次函数,其函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,A(0,-$\sqrt{2}$),点B为直线y=-x上一动点,当线段AB最短时,点B的坐标为( )
如图,A(0,-$\sqrt{2}$),点B为直线y=-x上一动点,当线段AB最短时,点B的坐标为( )| A. | (0,0) | B. | (1,-1) | C. | ($\frac{1}{2}$,-$\frac{1}{2}$) | D. | ($\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com