

分析 根据B类的人数,男女共25人,所占的百分比是50%,即可求得总人数;根据百分比的意义求得C类的人数,进而求得女生的人数,即可补全条形图,先求出样本中对火锅的评价在好及好以上的人数所占的百分比,再利用样本估计总体的思想即可求解.
解答 解:总人数为:(10+15)÷50%=50,
C类学生为:50×40%=20,
C类女生为:20-12=8,
补充条形统计图: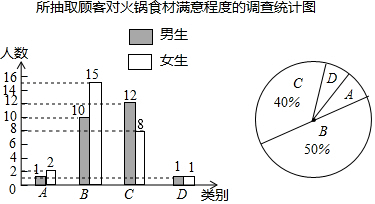
550×$\frac{1+2+10+15}{50}$=308.
故答案为50,308.
点评 本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.也考查了用样本估计总体的思想.


科目:初中数学 来源: 题型:选择题
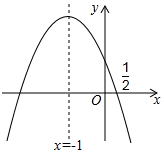 如图,抛物线y=ax2+bx+c的对称轴是x=-1.且过点($\frac{1}{2}$,0),有下列结论:①abc>0;
如图,抛物线y=ax2+bx+c的对称轴是x=-1.且过点($\frac{1}{2}$,0),有下列结论:①abc>0; | A. | ①②③ | B. | ①③④ | C. | ①②③⑤ | D. | ①③⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形ABCD是长方形(长方形对边相等且平行,四个角为直角),
如图,四边形ABCD是长方形(长方形对边相等且平行,四个角为直角),查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 问题呈现:
问题呈现:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com