
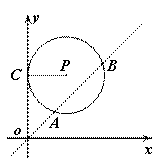
如图,在平面直角坐标系xOy中,⊙P与y轴
相切于点C,⊙P的半径是4,直线 被⊙P
被⊙P
截得的弦AB的长为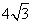 ,求点P的坐标.
,求点P的坐标.
解:延长CP交AB于点E,过点P做PD⊥AB于D
∴AD=BD= =
=
连接PA
在△PDA中,∠PDA=90°,PA=4,AD=
∴PD=2 ---------------------1分
∵⊙P与y轴相切于点C
 ∴PC⊥y轴,
∴PC⊥y轴,
∴∠OCE=90° ----------------2分
∵直线y=x,
∴∠COE=45° ------------------3分
∴∠CEO=45°,OC=CE
在△PDE中,∠PDE=90°,PD=2,∴PE=
∴CE=4+ ,∴OC=4+
,∴OC=4+ --------------------------------------4分
--------------------------------------4分
∴点P的坐标为:P(4,4+ )-------------------------------------5分
)-------------------------------------5分


科目:初中数学 来源: 题型:
有这样一个问题:探究函数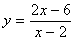 的图象与性质.
的图象与性质.
小慧根据学习函数的经验,对函数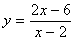 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小慧的探究过程,请补充完成:
(1)函数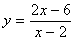 的自变量x的取值范围是___________;
的自变量x的取值范围是___________;
(2)列出y与x的几组对应值.请直接写出m的值,m=__________;
| x | … | -3 | -2 | 0 | 1 | 1.5 | 2.5 | m | 4 | 6 | 7 | … |
| y | … | 2.4 | 2.5 | 3 | 4 | 6 | -2 | 0 | 1 | 1.5 | 1.6 | … |
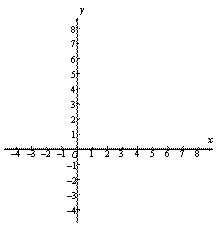
(3)请在平面直角坐标系 中,描出以上表中各对对应值为坐标的点,并画出该函数的图象;
中,描出以上表中各对对应值为坐标的点,并画出该函数的图象;
(4)结合函数的图象,写出该函数的两条性质:
① ;
 |
② .
查看答案和解析>>
科目:初中数学 来源: 题型:
.下表给出了代数式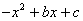 与
与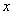 的一些对应值:
的一些对应值:
|
| …… | -2 | -1 | 0 | 1 | 2 | 3 | …… |
|
| …… | 5 |
| c | 2 | -3 | -10 | …… |
(1)根据表格中的数据,确定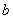 ,
,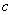 ,
,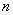 的值;
的值;
(2)设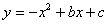 ,直接写出
,直接写出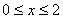 时
时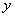 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
经专家测算,北京的4G网络速度基本上能够保证在80 000 000bps左右,最高峰值时曾达到106 000 000bps,将106 000 000用科学记数法表示应为
A.106×106 B.1.06×106 C.1.06×108 D.1.06×109
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,数轴上的点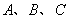 分别表示数
分别表示数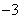 、
、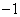 、
、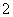 .
.
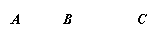

(1)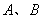 两点的距离
两点的距离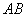 = ,
= ,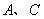 两点的距离AC= ;
两点的距离AC= ;
(2)通过观察,可以发现数轴上两点间距离与这两点表示的数的差的绝对值有一定关系,按照此关系,若点E表示的数为x,则AE= ;
(3)利用数轴直接写出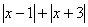 的最小值= .
的最小值= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com