

分析 (1)首先证明四边形CDBE是正方形,求出BE、AB,在Rt△ABE中,利用勾股定理即可解决问题.
(2)如图2中,延长AC、BE交于点M,连接DE,由△ACD≌△BCE,推出CD=CE,AD=BE,再证明BD=ME=2CF,在Rt△DBE中,根据BE2+BD2=BE2+EM2=BE2+(2CF)2=ED2,即可证明.
(3)如图3中,连接CM,过A作AN⊥CD于N,连接MN,首先证明△ACN≌△BCH,△CHM≌△ANM,推出MN=MH,∠HMN=∠HMA+∠NMA=∠HMA+∠HMC=∠CMA=90°,推出△HMN是等腰直角三角形,由CH:HB=1:5,设CH=x,HB=5x,则CB=$\sqrt{26}$x,推出CN=BH=5x,NH=CN-CH=4x,MH=2$\sqrt{2}$x,由此即可解决问题.
解答 (1)解:如图1中,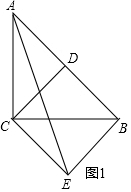
在Rt△ABC中,∵∠ACB=90°,AC=BC=4,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$,
∵AD=DB,
∴AD=DB=CD=2$\sqrt{2}$,CD⊥AB,
∵CD⊥CE,BD⊥BE,
∴∠DCE=∠EBD=∠CDB=90°,
∴四边形CDBE是矩形,
∵CD=BD,
∴四边形CDBE是正方形,
∴BE=CD=2$\sqrt{2}$,∠EBD=90°,
∴AE=$\sqrt{A{B}^{2}+B{E}^{2}}$=$\sqrt{(4\sqrt{2})^{2}+(2\sqrt{2})^{2}}$=2$\sqrt{10}$.
(2)如图2中,延长AC、BE交于点M,连接DE,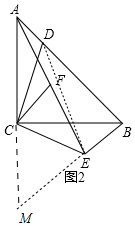
∵△ABC为等腰直角三角形,
∴∠BCA=∠BCM=90°,∠CAB=∠CBA=45°,AC=BC.
∵CD⊥CE,BD⊥BE,
∴∠ACB=∠DCE=90°,∠ABC=∠CBE=45°
∴∠ACD=∠BCE,∠CAD=∠CBE,
在△ACD和△BCE中,
$\left\{\begin{array}{l}{∠ACD=∠BCE}\\{AC=BC}\\{∠CAD=∠CBE}\end{array}\right.$,
∴△ACD≌△BCE,
∴CD=CE,AD=BE,
∵∠CBE=∠CMB=45°,
∴BC=CA=CM,
∵BC⊥AM,
∴BA=BM,
∵AC=CM,AF=FE,
∴ME=2CF,
∴AB-AD=BM-BE,
∴BD=ME=2CF,
在Rt△DBE中,BE2+BD2=BE2+EM2=BE2+(2CF)2=ED2,
即BE2+4CF2=($\sqrt{2}$CD)2=2CD2.
(3)如图3中,连接CM,过A作AN⊥CD于N,连接MN,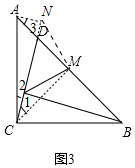
∵BH⊥CD,AN⊥CD,
∴∠ANC=∠BHC=90°,
∵∠2+∠BCH=90°,∠2+∠CAN=90°,
∴∠BCH=CAN,
在△ACN和△BCH中,
$\left\{\begin{array}{l}{∠ANC=∠BHC}\\{∠CAN=∠BCH}\\{AC=BC}\end{array}\right.$,
∴△ACN≌△BCH,
∴AN=CH,CN=BH,
∵MA=MB,∠ACB=90°,
∴CM=AM,∠CMA=90°,
∵∠AND=∠CMD=90°,∠ADN=∠CDM,
∴∠1=∠3,
∴△CHM≌△ANM,
∴MN=MH,∠HMN=∠HMA+∠NMA=∠HMA+∠HMC=∠CMA=90°,
∴△HMN是等腰直角三角形,
∵CH:HB=1:5,设CH=x,HB=5x,则CB=$\sqrt{26}$x,
∴CN=BH=5x,NH=CN-CH=4x,MH=2$\sqrt{2}$x,
∴$\frac{CB}{HM}$=$\frac{\sqrt{26}x}{2\sqrt{2}x}$=$\frac{\sqrt{13}}{2}$.
点评 本题考查三角形综合题、全等三角形的判定和性质、等腰直角三角形的判定和性质、勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形,学会利用参数解决问题,属于中考压轴题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
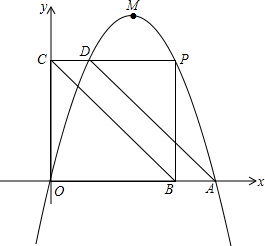 在平面直角坐标系xOy中,抛物线y=-x2+4x与x轴的正半轴交于点A,其顶点为M,点P是该抛物线上位于A、M两点之间的部分上的动点,过点P作PB⊥x轴于点B,PC⊥y轴于点C,且交抛物线于点D,连接BC,AD,OP,当四边形ABCD被OP分成的两部分面积比为1:2时,点P的坐标为($\frac{12}{5}$,$\frac{96}{25}$).
在平面直角坐标系xOy中,抛物线y=-x2+4x与x轴的正半轴交于点A,其顶点为M,点P是该抛物线上位于A、M两点之间的部分上的动点,过点P作PB⊥x轴于点B,PC⊥y轴于点C,且交抛物线于点D,连接BC,AD,OP,当四边形ABCD被OP分成的两部分面积比为1:2时,点P的坐标为($\frac{12}{5}$,$\frac{96}{25}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com