

分析 (1)要证明CE+AF=EF,只要作BM⊥EF,连接BF,构造出合适的三角形,然后根据角平分线的性质,证明三角形全等,进而得到边相等,进行合理的转化即可证得结论成立;
(2)要证明CE+AF=BE,要作辅助线延长DC到点H,使得CH=AF,然后根据题目中的条件进行灵活变化即可证得结论成立;
(3)要求BF的长,可以做出合适的辅助线,然后根据三角形相似,可以求得BF的长.
解答 (1)证明:作BM⊥EF于点M,连接BF,如由图1所示,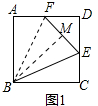
∵BE平分∠CEF,BC⊥CE,BM⊥EF,
∴BC=BM,∠BCE=∠BME=90°,
∵BE=BE,
∴△BCE≌△BME(HL),
∴CE=EM,
∵∠BMF=∠BAF=90°,BF=BF,BM=BA,
∴△BMF≌BAF(HL),
∴AF=MF,
∵EF=EM+MF,
∴CE+AF=EF;
(2)证明:延长DC到点H,使得CH=AF,如由图2所示,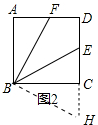
∵BA=BC,∠BAF=∠BCH=90°,AF=CH,
∴△BAF≌△BCH(SAS),
∴∠ABF=∠CBH,
∵∠CBH+∠CHB=90°,∠CBE+∠EBF+∠ABF=90°,BF平分∠ABE,
∴∠ABF=∠FBE,
∴∠HBC+∠CBE+∠ABF=90°,
∴∠CBH+∠HBE=90°,
∴∠CHB=∠HBE,
∴BE=EH,
∵EH=CE+CH,CH=AF,
∴CE+AF=BE;
(3)连接BD,作EM⊥BD于点M,如图3所示,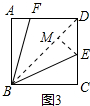
∵BC=6,BE=3$\sqrt{5}$,∠BCE=90°,
∴CE=$\sqrt{(3\sqrt{5})^{2}-{6}^{2}}=3$,
∴DE=6-3=3,
∵EM⊥BD,∠BDE=∠DBC=45°,
∴EM=DM=DE•sin45°=3×$\frac{\sqrt{2}}{2}$=$\frac{3\sqrt{2}}{2}$,
∵BC=CD=6,∠BCD=90°,
∴BD=6$\sqrt{2}$,
∴BM=$6\sqrt{2}-\frac{3\sqrt{2}}{2}=\frac{9\sqrt{2}}{2}$,
∵∠EBF=∠ABF+∠CBE,∠MBE+∠CBE=45°,∠ABC=∠EBF+∠ABF+∠CBE=90°
∴∠ABF+∠CBE=∠MBE+∠CBE=45°,
∴∠ABF=∠MBE,
∵∠BAF=∠BME=90°,
∴△ABF∽△MBE,
∴$\frac{AB}{MB}=\frac{BF}{BE}$,
即$\frac{6}{\frac{9\sqrt{2}}{2}}=\frac{BF}{3\sqrt{5}}$,
解得,BF=2$\sqrt{10}$.
点评 本题考查四边形综合题,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想和三角形相似、全等的知识进行解答.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:选择题
| A. | ($\frac{7}{18},\frac{5}{18}$) | B. | ($\frac{1}{2},\frac{2}{3}$) | C. | ($\frac{2}{3},\frac{1}{2}$) | D. | ($\frac{7}{6},\frac{5}{6}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,边长为a的正方形ABCD中,E,F是边AD,AB上两点(与端点不重合),且AE=BF,连接CE,DF相交于点M.
如图,边长为a的正方形ABCD中,E,F是边AD,AB上两点(与端点不重合),且AE=BF,连接CE,DF相交于点M.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 点P是等腰直角三角形ABC底边BC上一点,过点P作BA、AC的垂线,垂足为E、F,设D为BC的中点.
点P是等腰直角三角形ABC底边BC上一点,过点P作BA、AC的垂线,垂足为E、F,设D为BC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB是⊙O的一条弦,直径CD⊥AB于E,连接CA、CB,点M、N分别为CA、CB的中点,连接ME、NE.
如图,AB是⊙O的一条弦,直径CD⊥AB于E,连接CA、CB,点M、N分别为CA、CB的中点,连接ME、NE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com