
无锡春秋旅行社为吸引市民组团去天水湾风景区旅游,推出了如下收费标准:
某单位组织员工去天水湾风景区旅游,共支付给春秋旅行社旅游费用28000元,请问该单位这次共有多少员工去天水湾风景区旅游?
【考点】一元二次方程的应用.
【分析】首先分析得出这次旅游员工大体人数,因为支付给春秋旅行社旅游费用为28000元,当旅游人数是30时,30×800=24000元,低于28000元,可得出实际人数超过了30人,再表示出每人应交钱数800﹣(x﹣30)×10,结合实际问题列出方程求出即可.
【解答】解:∵支付给春秋旅行社旅游费用为28000元,当旅游人数是30时,30×800=24000元,低于28000元.
∴这次旅游超过了30人.
∴假设这次旅游员工人数为x人,根据题意列出方程得:
∵[800﹣(x﹣30)×10]x=28000,
∴x2﹣110x+2800=0,
解得:x1=40,x2=70,
当x1=40时,800﹣10(x﹣30)=700>700(符合题意)
当x2=70时,800﹣10(x﹣30)=400<500(不合题意,舍去)
答:该单位这次共有40员工去天水湾风景区旅游.
【点评】此题主要考查了一元二次方程的解法及应用,关键是表示出参加旅游每人所付费用是解决问题的关键.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
如图,图中的小方格都是边长为1的正方形,△ABC的A、B、C三点坐标为A(2,0)、B(2,2)、C(6,3)。
(1) 请在图中画出一个△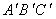 ,使△
,使△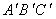 与△ABC是以坐标原点为位似中心,相似比为2的位似图形。
与△ABC是以坐标原点为位似中心,相似比为2的位似图形。
(2)求△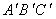 的面积。
的面积。

查看答案和解析>>
科目:初中数学 来源: 题型:
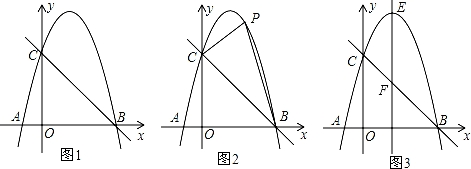
如图1,抛物线y=ax2+bx﹣4a经过A(﹣1,0)、C(0,4)两点,与x轴交于另一点B.
(1)求抛物线的解析式;
(2)已知点D(m,m+1)在第一象限的抛物线上,求点D关于直线BC对称的点的坐标;
(3)如图2,点P为第一象限抛物线上一点,是否存在使△PBC面积最大的点P?若存在,求出点P的坐标;若不存在,请说明理由;
(4)如图3,若抛物线的对称轴EF(E为抛物线顶点)与直线BC相交于点F,M为直线BC上的任意一点,过点M作MN∥EF交抛物线于点N,以E,F,M,N为顶点的四边形能否为平行四边形?若能,求点N的坐标;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com