
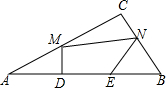
 如图,Rt△ABC中,∠C=90°,点D、E为边AB上的点,且AD=BE,点M、N分别为边AC、BC上的点,已知AB=a,DE=b,则四边形DMNE的周长的最小值为( )
如图,Rt△ABC中,∠C=90°,点D、E为边AB上的点,且AD=BE,点M、N分别为边AC、BC上的点,已知AB=a,DE=b,则四边形DMNE的周长的最小值为( )| A. | a | B. | 2a-b | C. | a+b | D. | a+2b |
分析 作点D关于AC的对称点G,点E关于BC的对称点H,连接AG、BH、GH,GH与AC交于点M,与BC交于点N,此时四边形DMNE的周长=DM+MN+NE+DE=GM+MN+NH+DE=GH+DE最小,接下来只要证明四边形AGHB是平行四边形即可解决问题.
解答 解:如图作点D关于AC的对称点G,点E关于BC的对称点H,连接AG、BH、GH,GH与AC交于点M,与BC交于点N,
此时四边形DMNE的周长=DM+MN+NE+DE=GM+MN+NH+DE=GH+DE最小(两点之间线段最短),
∵AG=AD,BE=BH,AD=EB,
∴AG=BH,
∵∠C=90°,
∴∠CAB+∠CBA=90°,
∵∠GAM=∠CAB,∠CBH=∠CBA,
∴∠GAB+∠HBA=180°,
∴AG∥BH,
∴四边形AGHB是平行四边形,
∴GH=AB=a,
∴四边形DMNE的周长的最小值=GH+DE=a+b.
故选C.
点评 本题考查轴对称-最短问题、两点之间线段最短等知识,解题的关键利用轴对称性质,根据两点之间线段最短正确找到点M、N的位置,属于中考常考题型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,正方形ABCD的边长为8cm,E、F、G、H分别是AB、BC、CD、DA 上的动点,且AE=BF=CG=DH.
如图,正方形ABCD的边长为8cm,E、F、G、H分别是AB、BC、CD、DA 上的动点,且AE=BF=CG=DH.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=$\sqrt{5}$ b=2 c=3 | B. | a=7 b=24 c=5 | C. | a=6 b=8 c=10 | D. | a=3 b=4 c=5 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
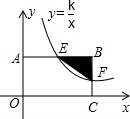 如图,反比例函数y=$\frac{k}{x}$(k>0)的图象与矩形ABCO的两边相交于E,F两点,若E是AB的中点,S△BEF=1,则k的值为4.
如图,反比例函数y=$\frac{k}{x}$(k>0)的图象与矩形ABCO的两边相交于E,F两点,若E是AB的中点,S△BEF=1,则k的值为4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ②④ | C. | ①②③ | D. | ①③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com