
【题目】已知一次函数y=(1-2m)x+m+1(m≠![]() ),函数值y随自变量x值的增大而减小.
),函数值y随自变量x值的增大而减小.
(1)求m的取值范围;
(2)在平面直角坐标系xOy中,这个函数的图象与x轴的交点M位于x轴的正半轴还是负半轴?请简述理由.
【答案】(1)m>![]() ;(2)这个函数的图象与x轴的交点M位于x轴的正半轴.
;(2)这个函数的图象与x轴的交点M位于x轴的正半轴.
【解析】
(1)由一次函数图象与系数的关系得到:1-2m<0,由此求得m的取值范围;
(2)令y=0,得到关于(1-2m)x+m+1=0,结合m的取值范围求得x的符号.
解:(1)∵一次函数y=(1-2m)x+m+1(m≠![]() ),函数值y随自变量x值的增大而减小,
),函数值y随自变量x值的增大而减小,
∴1-2m<0,
解得m>![]() ;
;
(2)在平面直角坐标系xOy中,这个函数的图象与x轴的交点M位于x轴的正半轴.
理由:令y=0,则(1-2m)x+m+1=0,
整理,得x=![]()
由(1)知,m>![]() ,则m+1>0,2m-1>0,
,则m+1>0,2m-1>0,
∴x=![]() >0,
>0,
∴在平面直角坐标系xOy中,这个函数的图象与x轴的交点M位于x轴的正半轴.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是边AB上的一动点(不与点A、B重合),连接DE,点A关于直线DE的对称点为F,连接EF并延长交BC于点G,连接DG,过点E作EH⊥DE交DG的延长线于点H,连接BH.
(1)求证:GF=GC;
(2)用等式表示线段BH与AE的数量关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
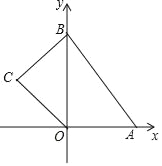
【题目】如图,在平面直角坐标系中,四边形OABC的顶点O是坐标原点,点A的坐标为(6,0),点B的坐标为(0,8),点C的坐标为(﹣2![]() ,4),点M,N分别为四边形OABC边上的动点,动点M从点O开始,以每秒1个单位长度的速度沿O→A→B路线向终点B匀速运动,动点N从O点开始,以每秒两个单位长度的速度沿O→C→B→A路线向终点A匀速运动,点M,N同时从O点出发,当其中一点到达终点后,另一点也随之停止运动,设动点运动的时间t秒(t>0),△OMN的面积为S.
,4),点M,N分别为四边形OABC边上的动点,动点M从点O开始,以每秒1个单位长度的速度沿O→A→B路线向终点B匀速运动,动点N从O点开始,以每秒两个单位长度的速度沿O→C→B→A路线向终点A匀速运动,点M,N同时从O点出发,当其中一点到达终点后,另一点也随之停止运动,设动点运动的时间t秒(t>0),△OMN的面积为S.
(1)填空:AB的长是 ,BC的长是 ;
(2)当t=3时,求S的值;
(3)当3<t<6时,设点N的纵坐标为y,求y与t的函数关系式;
(4)若S=![]() ,请直接写出此时t的值.
,请直接写出此时t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
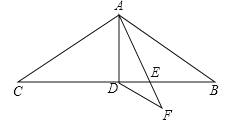
【题目】如图在△ABC中,AB=AC=9,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是直线l外一点,A,B,C三点在直线l上,且PB⊥l于点B,∠APC=90°,则下列结论:①线段AP是点A到直线PC的距离;②线段BP的长是点P到直线l的距离;③PA,PB,PC三条线段中,PB最短;④线段PC的长是点P到直线l的距离,其中,正确的是( )

A. ②③ B. ①②③ C. ③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AB的垂直平分线DE交AC于D,垂足为E,若∠A=30°,CD=3.

(1)求∠BDC的度数.
(2)求AC的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的两边BC,AB分别在平面直角坐标系的x轴、y轴的正半轴上,正方形A′B′C′D′与正方形ABCD是以AC的中点O′为中心的位似图形,已知AC=3![]() ,若点A′的坐标为(1,2),则正方形A′B′C′D′与正方形ABCD的相似比是( )
,若点A′的坐标为(1,2),则正方形A′B′C′D′与正方形ABCD的相似比是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算张老师在黑板上写了三个算式,希望同学们认真观察,发现规律.

请你结合这些算式,解答下列问题:
(1)请你再写出另外两个符合上述规律的算式;
(2)验证规律:设两个连续奇数为2n+1,2n–1(其中n为正整数),则它们的平方差是8的倍数;
(3)拓展延伸:“两个连续偶数的平方差是8的倍数”,这个结论正确吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com