
【题目】如图,在△ABC中,AB=AC,AD和BE是高,它们相交于点H,且AE=BE
求证:AH=2BD

科目:初中数学 来源: 题型:
【题目】某生活小区鲜奶店每天以每瓶3元的价格从奶场购进优质鲜奶,然后以每瓶6元的价格出售,如果当天卖不完,剩余的只有倒掉.店主记录了30天的日需求量(单位:瓶),整理得下表:
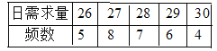
(1)求这30天内日需求量的众数;
(2)假设鲜奶店在这30天内每天购进28瓶,求这30天的日利润(单位:元)的平均数;
(3)以30记录的各需求量的频率作为各需求是发生的概率.若鲜奶店每天购进28瓶,求在这记录的30天内日利润不低于81元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数y=![]() (k为常数,且k≠0)的图象经过点A(1,3)、B(3,m).
(k为常数,且k≠0)的图象经过点A(1,3)、B(3,m).
(1)求反比例函数的解析式及B点的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
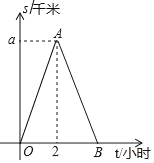
【题目】小明从家出发沿滨江路到外滩公园徒步锻炼,到外滩公园后立即沿原路返回,小明离开家的路程s(单位:千米)与走步时间t(单位:小时)之间的函数关系如图所示,其中从家到外滩公园的平均速度是4千米/时,根据图形提供的信息,解答下列问题:
(1)求图中的a值;
(2)若在距离小明家5千米处有一个地点C,小明从第一层经过点C到第二层经过点C,所用时间为1.75小时,求小明返回过程中,s与t的函数解析式,不必写出自变量的取值范围;
(3)在(2)的条件下,求小明从出发到回到家所用的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC中,AB=AC=10cm,BC=12cm,D为BC上一点,连接AD,E为AD上一点,连接BE,若∠ABE=∠BAE═![]() ∠BAC,则DE的长为( )
∠BAC,则DE的长为( )

A.![]() cmB.
cmB.![]() cmC.
cmC.![]() cmD.1cm
cmD.1cm
查看答案和解析>>
科目:初中数学 来源: 题型:
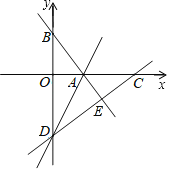
【题目】如图,在平面直角坐标系中,直线AB与x轴、y轴分别交于点A(3,0)、B(0,4),点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
(1)求直线AB的表达式;
(2)求点C和点D的坐标;
(3)y轴的正半轴上是否存在一点P,使得S△PAB=![]() S△OCD?若存在,求出点P的坐标;若不存在,请说明理由.
S△OCD?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
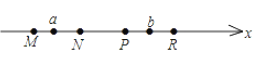
【题目】如图,![]() 分别是数轴上四个整数所对应的点,其中有一点是原点,并且这四个整数点每相邻两点之间的距离为1个单位长度.数
分别是数轴上四个整数所对应的点,其中有一点是原点,并且这四个整数点每相邻两点之间的距离为1个单位长度.数![]() 对应的点在
对应的点在![]() 与
与![]() 之间,数
之间,数![]() 对应的点在
对应的点在![]() 与
与![]() 之间.若
之间.若![]() ,则原点是( )
,则原点是( )
A.![]() 或
或![]() B.
B.![]() 与
与![]() C.
C.![]() 与
与![]() D.
D.![]() 与
与![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线AB∥CD,直线EF分别交AB、CD于A、C,CM是∠ACD的平分线,CM交AB于H,过A作AG⊥AC交CM于G.
(1)如图1,点G在CH的延长线上时,
①若∠GAB=36°,则∠MCD=______.
②猜想:∠GAB与∠MCD之间的数量关系是______.
(2)如图2,点G在CH上时,(1)②猜想的∠GAB与∠MCD之间的数量关系还成立吗?如果成立,请给出证明;如果不成立,请写出∠GAB与∠MCD之间的数量关系,并说明理由.
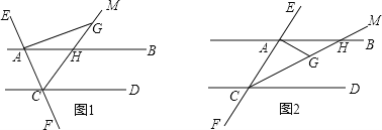
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com