
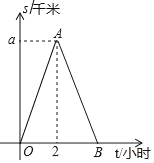
����Ŀ��С���Ӽҳ����ر���·����̲��ͽ������������̲����������ԭ·���أ�С���뿪�ҵ�·��s����λ��ǧ�ף����߲�ʱ��t����λ��Сʱ��֮��ĺ�����ϵ��ͼ��ʾ�����дӼҵ���̲����ƽ���ٶ���4ǧ��/ʱ������ͼ���ṩ����Ϣ������������⣺
��1����ͼ�е�aֵ��
��2�����ھ���С����5ǧ�״���һ���ص�C��С���ӵ�һ�㾭����C���ڶ��㾭����C������ʱ��Ϊ1.75Сʱ����С�����ع����У�s��t�ĺ�������ʽ������д���Ա�����ȡֵ��Χ��
��3���ڣ�2���������£���С���ӳ������ص������õ�ʱ�䣮
���𰸡���1��8����2��s=��3t+14����3��С���ӳ������ص������õ�ʱ����![]() Сʱ��
Сʱ��
������������: ��1������·��=�ٶ���ʱ�伴�����aֵ��
��2�������ٶ�=·����ʱ��������˷���ʱ���ٶȣ��ٸ���·��=8-����ʱ���ٶ���ʱ�伴�ɵó�AB����ֱ�ߵĺ�������ʽ��
��3������2���еĺ�����ϵʽ��s=0�����tֵ���ɣ�
���:
��1��������ɵã�
a=2��4=8��
��a��ֵ��8��
��2��������ɵã�
С���Ӽҵ����Ĺ����У�C�㵽A���õ�ʱ��Ϊ����8��5����4=0.75Сʱ��
С���ӹ����ҵĹ����У�A�㵽C���õ�ʱ��Ϊ1.75��0.75=1Сʱ���ٶ�Ϊ����8��5����1=3ǧ��/ʱ��
��С���ӹ������õ�ʱ��Ϊ��8��3=![]() Сʱ��
Сʱ��
���A��2��8������B��![]() ��0��
��0��
��С�����ع����У�s��t�ĺ�������ʽ��s=kt+b��
 ����
����![]()
��С�����ع����У�s��t�ĺ�������ʽ��s=��3t+14��
��3����s=0ʱ����3t+14=0����t=![]() ��
��
��С���ӳ������ص������õ�ʱ����![]() Сʱ��
Сʱ��
�㾦: ���⿼��һ�κ�����Ӧ�ã������Ĺؼ�����ȷ���⣬�����Ӧ�ĺ�������ʽ�����ú�����˼������ν�ϵ�˼����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������С��ͬ�ĵ���ֱ�����ǰ���ͼ1��ʾ���ã�ͼ2������������ļ���ͼ�Σ�ͼ��AB=AC��AD=AE����BAC=��EAD=90����B,C,E��ͬһ��ֱ���ϣ�����DC��
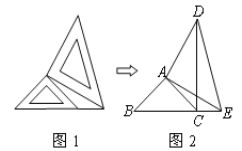
��1��ͼ2�е�ȫ����������_______________,������֤����˵���������в��ú���δ��ʶ����ĸ����
��2��ָ���߶�DC���߶�BE�Ĺ�ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ǽ�϶�����һ������Χ�ɵ�������״�������ͼʵ����ʾ����λ��cm����Сӱ�������µĶ���ȥ��������������������һ�������Σ���ͼ������ʾ��Сӱ���������εij�������Ϊ�������ף�����賤���εij�Ϊxcm���������⣬�ɵ÷���Ϊ��������
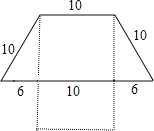
A.2��x+10����10��4+6��2B.2��x+10����10��3+6��2
C.2x+10��10��4+6��2D.2��x+10����10��2+6��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
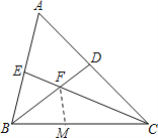
����Ŀ���ڡ�ABC�У���A=60����BD��CE�ǡ�ABC��������ƽ���ߣ���BD��CE���ڵ�F����ͼ��ʾ���õ�ʽ��ʾBE��BC��CD�������߶�֮���������ϵ����֤����Ľ��ۣ�
����ͨ���۲죬ʵ�飬������룺BE+CD=BC������������BC�Ͻ�ȡBM��ʹBM=BE������FM��������������ȫ�ȵ��ж�������֤��CM=CD���ɣ�
��1��������С��֤���ò���IJ���˼·���벹��������
����BC�Ͻ�ȡBM��ʹBM=BE������FM�������֤����BEF��______ȫ�ȣ��ж�����ȫ�ȵ�������______��
���ɡ�A=60����BD��CE�ǡ�ABC��������ƽ���ߣ����Եó���EFB=______����
��2����ֱ�����â٣����ѵõ��Ľ��ۣ����֤������BE+CD=BC�Ĺ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һԲ������ı�ֱ����![]() �������涨ֱ�����ȵ�����(����)��������������涨ֱ�����ȵ�����(����)��������������Աij�γ���������Ʒ�����Ľ�����£�
�������涨ֱ�����ȵ�����(����)��������������涨ֱ�����ȵ�����(����)��������������Աij�γ���������Ʒ�����Ľ�����£�
��� |
|
|
|
|
|
ֱ������/ |
|
|
|
|
|
��1����ָ���ļ���Ʒ�Ĵ�С�����Ҫ��
��2������涨���ľ���ֵ��![]() ֮������Ʒ.���ľ���ֵ��
֮������Ʒ.���ľ���ֵ��![]() ֮���Ǵ�Ʒ�����ľ���ֵ����
֮���Ǵ�Ʒ�����ľ���ֵ����![]() ���Ƿ�Ʒ����ô���������Ʒ�У���Щ����Ʒ����Щ�Ǵ�Ʒ����Щ�Ƿ�Ʒ��
���Ƿ�Ʒ����ô���������Ʒ�У���Щ����Ʒ����Щ�Ǵ�Ʒ����Щ�Ƿ�Ʒ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ�����������ѧ���ؾ��ص�������������¡������������һ���⣺������ɳ��һ�飬����б������Сб�����бʮ�����бʮ�����֪Ϊ�X�Σ�������⽲���ǣ���һ��������ɳ������߳��ֱ�Ϊ5�12�13������ɳ������ж���������������ҹ����Ƴ��ȵ�λ��1��=500�ף����ɳ������Ϊ��������
A. 7.5ƽ��ǧ�� B. 15ƽ��ǧ�� C. 75ƽ��ǧ�� D. 750ƽ��ǧ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB��AC��AD��BE�Ǹߣ������ཻ�ڵ�H����AE��BE
��֤��AH��2BD

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��AB=AC��AE=AF������BF��CE������O������AO����֤��
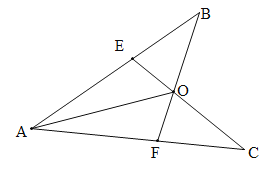
��1����B=��C
��2��AOƽ����BAC
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��2��A�ͳ���1��B�ͳ���������һ�ο��˻���10�֣���1��A�ͳ���2��B�ͳ���������һ�ο��˻�11�֣�ij������˾����31�ֻ���ƻ�ͬʱ����A�ͳ�a����B�ͳ�b����һ�����꣬��ǡ��ÿ�����������������������Ϣ������������⣺
��1����1��A�ͳ���1��B�ͳ�����������һ�οɷֱ��˻����ٶ֣�
��2��������������˾������������A�ͳ�ÿ�������100Ԫ/�Σ�B�ͳ�ÿ�������120Ԫ/�Σ���ѡ����ʡǮ��������������������ѣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com