
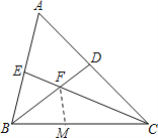
【题目】在△ABC中,∠A=60°,BD,CE是△ABC的两条角平分线,且BD,CE交于点F,如图所示,用等式表示BE,BC,CD这三条线段之间的数量关系,并证明你的结论;
晓东通过观察,实验,提出猜想:BE+CD=BC,他发现先在BC上截取BM,使BM=BE,连接FM,再利用三角形全等的判定和性质证明CM=CD即可.
(1)下面是小东证明该猜想的部分思路,请补充完整;
①在BC上截取BM,使BM=BE,连接FM,则可以证明△BEF与______全等,判定它们全等的依据是______;
②由∠A=60°,BD,CE是△ABC的两条角平分线,可以得出∠EFB=______°;
(2)请直接利用①,②已得到的结论,完成证明猜想BE+CD=BC的过程.
【答案】(1)①△BMF,SAS;②60;(2)见解析
【解析】
(1)①由BD,CE是△ABC的两条角平分线知∠FBE=∠FBC=![]() ∠ABC,结合BE=BM,BF=BF,依据“SAS”即可证得△BEF≌△BMF;
∠ABC,结合BE=BM,BF=BF,依据“SAS”即可证得△BEF≌△BMF;
②利用三角形内角和求出∠ABC+∠ACB=120°,进而得出∠FBC+∠FCB=60°,得出∠BFC=120°,即可得出结论;
(2)利用角平分线得出∠EBF=∠MBF,进而得出△BEF≌△BMF,求出∠BFM,即可判断出∠CFM=∠CFD,即可判断出△FCM≌△FCD,即可得出结论.
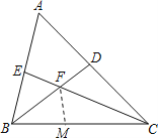
(1)解:①在BC上取一点M,使BM=BE,连接FM,如图所示:
∵BD、CE是△ABC的两条角平分线,
∴∠FBE=∠FBM=![]() ∠ABC,
∠ABC,
在△BEF和△BMF中,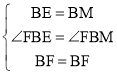 ,
,
∴△BEF≌△BMF(SAS),
故答案为:△BMF,SAS;
②∵BD、CE是△ABC的两条角平分线,
∴∠FBC+FCB=![]() (∠ABC+∠ACB),
(∠ABC+∠ACB),
在△ABC中,∠A+∠ABC+∠ACB=180°,
∵∠A=60°,
∴∠ABC+∠ACB=180°-∠A=180°-60°=120°,
∴∠BFC=180°-(∠FBC+∠FCB)=180°-![]() (∠ABC+∠ACB)=180°-
(∠ABC+∠ACB)=180°-![]() ×120°=120°,
×120°=120°,
∴∠EFB=60°,
故答案为:60;
(2)证明:由①知,∠BFE=60°,
∴∠CFD=∠BFE=60°
∵△BEF≌△BMF,
∴∠BFE=∠BFM=60°,
∴∠CFM=∠BFC-∠BFM=120°-60°=60°,
∴∠CFM=∠CFD=60°,
∵CE是∠ACB的平分线,
∴∠FCM=∠FCD,
在△FCM和△FCD中,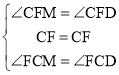 ,
,
∴△FCM≌△FCD(ASA),
∴CM=CD,
∴BC=CM+BM=CD+BE,
∴BE+CD=BC.


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
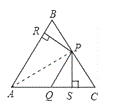
【题目】如图,在△ABC中,点P、Q分别是BC、AC边上的点,PS![]() AC,PR
AC,PR![]() AB,若
AB,若![]() ,PR
,PR![]() PS,则下列结论:①PA平分
PS,则下列结论:①PA平分![]() ,②AS
,②AS![]() AR;③QP∥AR;④△BRP≌△CPS;其中正确的结论有( )
AR;③QP∥AR;④△BRP≌△CPS;其中正确的结论有( )
A. 4个B. 3个C. 2个D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究下面的问题:
(1)如图甲,在边长为a的正方形中去掉一个边长为b的小正方形(a>b),把余下的部分剪拼成如图乙的一个长方形,通过计算两个图形(阴影部分)的面积,验证了一个等式,这个等式是________(用式子表示),即乘法公式中的___________公式.
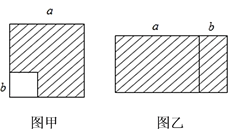
(2)运用你所得到的公式计算:
①10.7×9.3
②![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
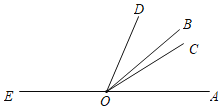
【题目】如图,点O是直线AE上的一点,OC是∠AOD的平分线,∠BOD=![]() ∠AOD.
∠AOD.
(1)若∠BOD=20°,求∠BOC的度数;
(2)若∠BOC=n°,用含有n的代数式表示∠EOD的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数y=![]() (k为常数,且k≠0)的图象经过点A(1,3)、B(3,m).
(k为常数,且k≠0)的图象经过点A(1,3)、B(3,m).
(1)求反比例函数的解析式及B点的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
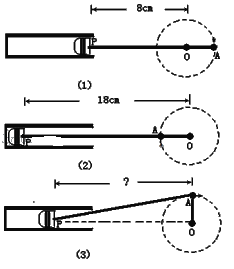
【题目】如图,曲柄连杆装置是很多机械上不可缺少的,曲柄OA绕O点圆周运动,连杆AP拉动活塞作往复运动.当曲柄的A旋转到最右边时,如图(1),OP长为8cm;当曲柄的A旋转到最左边时,如图(2)OP长为18cm.
(1)求曲柄OA和连杆AP分别有多长;
(2)求:OA⊥OP时,如图(3),OP的长是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
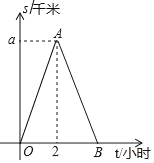
【题目】小明从家出发沿滨江路到外滩公园徒步锻炼,到外滩公园后立即沿原路返回,小明离开家的路程s(单位:千米)与走步时间t(单位:小时)之间的函数关系如图所示,其中从家到外滩公园的平均速度是4千米/时,根据图形提供的信息,解答下列问题:
(1)求图中的a值;
(2)若在距离小明家5千米处有一个地点C,小明从第一层经过点C到第二层经过点C,所用时间为1.75小时,求小明返回过程中,s与t的函数解析式,不必写出自变量的取值范围;
(3)在(2)的条件下,求小明从出发到回到家所用的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
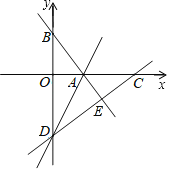
【题目】如图,在平面直角坐标系中,直线AB与x轴、y轴分别交于点A(3,0)、B(0,4),点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
(1)求直线AB的表达式;
(2)求点C和点D的坐标;
(3)y轴的正半轴上是否存在一点P,使得S△PAB=![]() S△OCD?若存在,求出点P的坐标;若不存在,请说明理由.
S△OCD?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
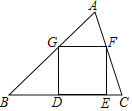
【题目】如图,已知正方形DEFG的顶点D、E在△ABC的边BC上,顶点G、F分别在边AB、AC上.如果BC=4,△ABC的面积是6,那么这个正方形的边长是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com