
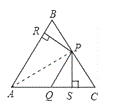
【题目】如图,在△ABC中,点P、Q分别是BC、AC边上的点,PS![]() AC,PR
AC,PR![]() AB,若
AB,若![]() ,PR
,PR![]() PS,则下列结论:①PA平分
PS,则下列结论:①PA平分![]() ,②AS
,②AS![]() AR;③QP∥AR;④△BRP≌△CPS;其中正确的结论有( )
AR;③QP∥AR;④△BRP≌△CPS;其中正确的结论有( )
A. 4个B. 3个C. 2个D. 1个
【答案】B
【解析】
根据角平分线判定定理即可推出①,根据勾股定理即可推出②AR=AS,根据等腰三角形性质推出∠QAP=∠QPA,推出∠QPA=∠BAP,根据平行线判定推出③QP∥AB即可;无法证明△BRP≌△CSP故④错误.
∵PR⊥AB,PS⊥AC,PR=PS,
∴点P在∠A的平分线上,故①正确,
∠ARP=∠ASP=90°,
∴∠SAP=∠RAP,
在Rt△ARP和Rt△ASP中,由勾股定理得:AR2=AP2-PR2,AS2=AP2-PS2,
∵AP=AP,PR=PS,
∴AR=AS,∴②正确;
∵AQ=QP,
∴∠QAP=∠QPA,
∵∠QAP=∠BAP,
∴∠QPA=∠BAP,
∴QP∥AR,∴③正确;
在△BRP和△CSP中,缺少全等条件,故④错误,
故选B.


科目:初中数学 来源: 题型:
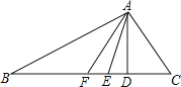
【题目】 如图,AD,AE和AF分别是△ABC的高、角平分线和中线.
(1)对于下面的五个结论:①BC=2BF;②∠CAE=![]() ∠CAB;③BE=CE;④AD⊥BC;⑤S△AFB=S△ADC.其中错误的是______(只填序号);
∠CAB;③BE=CE;④AD⊥BC;⑤S△AFB=S△ADC.其中错误的是______(只填序号);
(2)若∠C=70°,∠ABC=28°,求∠DAE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小刚相约周末到雪莲大剧院看演出,他们的家分别距离剧院1200m和2000m,两人分别从家中同时出发,已知小明和小刚的速度比是3:4,结果小明比小刚提前4min到达剧院.求两人的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
已知![]() ,
,![]() ,
,![]() ,…
,…![]() 都是不等于0的有理数,若
都是不等于0的有理数,若![]() ,求
,求![]() 的值.
的值.
解:当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,所以
,所以![]() 参照以上解答,试探究以下问题:
参照以上解答,试探究以下问题:
(1)若![]() ,求
,求![]() 的值
的值
(2)若![]() ,则
,则![]() 的值为__________;
的值为__________;
(3)由(1)、(2)试猜想,![]() 共有__________个不同的值,在
共有__________个不同的值,在![]() 这些不同的值中,最大的值和最小的值的差等于__________.
这些不同的值中,最大的值和最小的值的差等于__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学的高中部在A校区,初中部在B校区,学校学生会计划在3月12日植树节当天安排部分学生到郊区公园参加植树活动.已知A校区的每位高中学生往返车费是6元,B校区的每位初中学生往返的车费是10元,要求初、高中均有学生参加,且参加活动的初中学生比参加活动的高中学生多4人,本次活动的往返车费总和不超过210元,求初、高中最多各有多少学生参加.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个大小不同的等腰直角三角板如图1所示放置,图2是由它抽象出的几何图形,图中AB=AC,AD=AE,∠BAC=∠EAD=90°,B,C,E在同一条直线上,连结DC.
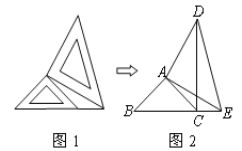
(1)图2中的全等三角形是_______________,并给予证明(说明:结论中不得含有未标识的字母);
(2)指出线段DC和线段BE的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=108°,EF、MN分别是AB、AC的垂直平分线,点E、N在BC上,则∠EAN等于( )
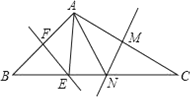
A. 72°B. 54°C. 36°D. 18°
查看答案和解析>>
科目:初中数学 来源: 题型:
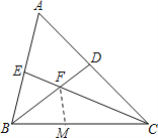
【题目】在△ABC中,∠A=60°,BD,CE是△ABC的两条角平分线,且BD,CE交于点F,如图所示,用等式表示BE,BC,CD这三条线段之间的数量关系,并证明你的结论;
晓东通过观察,实验,提出猜想:BE+CD=BC,他发现先在BC上截取BM,使BM=BE,连接FM,再利用三角形全等的判定和性质证明CM=CD即可.
(1)下面是小东证明该猜想的部分思路,请补充完整;
①在BC上截取BM,使BM=BE,连接FM,则可以证明△BEF与______全等,判定它们全等的依据是______;
②由∠A=60°,BD,CE是△ABC的两条角平分线,可以得出∠EFB=______°;
(2)请直接利用①,②已得到的结论,完成证明猜想BE+CD=BC的过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com