
【题目】探究下面的问题:
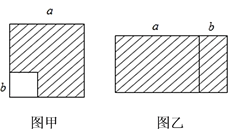
(1)如图甲,在边长为a的正方形中去掉一个边长为b的小正方形(a>b),把余下的部分剪拼成如图乙的一个长方形,通过计算两个图形(阴影部分)的面积,验证了一个等式,这个等式是________(用式子表示),即乘法公式中的___________公式.
(2)运用你所得到的公式计算:
①10.7×9.3
②![]()
【答案】(1)a2-b2=(a+b)(a-b);平方差;(2)①99.51;②x2-6xz+9z2-4y2.
【解析】
(1)这个图形变换可以用来证明平方差公式:已知在左图中,大正方形减小正方形剩下的部分面积为a2-b2;因为拼成的长方形的长为(a+b),宽为(a-b),根据“长方形的面积=长×宽”代入为:(a+b)×(a-b),因为面积相等,进而得出结论.
(2)①将10.7×9.3化为(10+0.7)×(10-0.7),再用平方差公式求解即可.
②利用平方差公式和完全平方公式求解即可.
(1) 由图知:大正方形减小正方形剩下的部分面积为a2-b2;
拼成的长方形的面积:(a+b)×(ab),所以得出:a2-b2=(a+b)(ab);
故答案为:a2-b2=(a+b)(ab);平方差
(2)①原式=(10+0.7)×(10-0.7)
=102-0.72
=100-0.49
=99.51.
②原式=(x-3z+2y)(x-3z-2y)
=(x-3z)2-(2y)2
=x2-6xz+9z2-4y2.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】小明和小刚相约周末到雪莲大剧院看演出,他们的家分别距离剧院1200m和2000m,两人分别从家中同时出发,已知小明和小刚的速度比是3:4,结果小明比小刚提前4min到达剧院.求两人的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个大小不同的等腰直角三角板如图1所示放置,图2是由它抽象出的几何图形,图中AB=AC,AD=AE,∠BAC=∠EAD=90°,B,C,E在同一条直线上,连结DC.
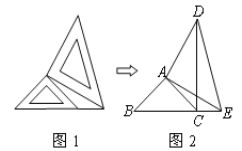
(1)图2中的全等三角形是_______________,并给予证明(说明:结论中不得含有未标识的字母);
(2)指出线段DC和线段BE的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=108°,EF、MN分别是AB、AC的垂直平分线,点E、N在BC上,则∠EAN等于( )
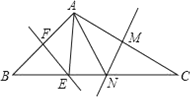
A. 72°B. 54°C. 36°D. 18°
查看答案和解析>>
科目:初中数学 来源: 题型:
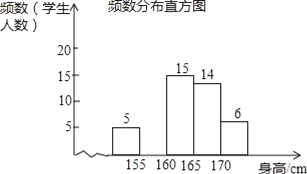
【题目】为了解某校九年级学生的身高情况,随机抽取部分学生的身高进行调查,利用所得数据绘成如图统计图表:
频数分布表
身高分组 | 频数 | 百分比 |
x<155 | 5 | 10% |
155≤x<160 | a | 20% |
160≤x<165 | 15 | 30% |
165≤x<170 | 14 | b |
x≥170 | 6 | 12% |
总计 | 100% |
(1)填空:a=____,b=____;
(2)补全频数分布直方图;
(3)该校九年级共有600名学生,估计身高不低于165cm的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,过点O作两条射线OM、ON,且∠AOM=∠CON=90°

(1)若OC平分∠AOM,求∠AOD的度数.
(2)若∠1=![]() ∠BOC,求∠AOC和∠MOD.
∠BOC,求∠AOC和∠MOD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】墙上钉着用一根彩绳围成的梯形形状的饰物,如图实线所示(单位:cm).小颖将梯形下底的钉子去掉,并将这条彩绳钉成一个长方形,如图虚线所示.小颖所钉长方形的长、宽各为多少厘米?如果设长方形的长为xcm,根据题意,可得方程为( )
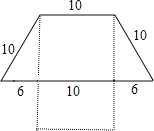
A.2(x+10)=10×4+6×2B.2(x+10)=10×3+6×2
C.2x+10=10×4+6×2D.2(x+10)=10×2+6×2
查看答案和解析>>
科目:初中数学 来源: 题型:
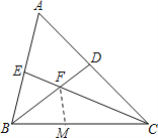
【题目】在△ABC中,∠A=60°,BD,CE是△ABC的两条角平分线,且BD,CE交于点F,如图所示,用等式表示BE,BC,CD这三条线段之间的数量关系,并证明你的结论;
晓东通过观察,实验,提出猜想:BE+CD=BC,他发现先在BC上截取BM,使BM=BE,连接FM,再利用三角形全等的判定和性质证明CM=CD即可.
(1)下面是小东证明该猜想的部分思路,请补充完整;
①在BC上截取BM,使BM=BE,连接FM,则可以证明△BEF与______全等,判定它们全等的依据是______;
②由∠A=60°,BD,CE是△ABC的两条角平分线,可以得出∠EFB=______°;
(2)请直接利用①,②已得到的结论,完成证明猜想BE+CD=BC的过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com