
【题目】已知:如图,AB=AC,AE=AF,连结BF,CE,交于O,连结AO.求证:
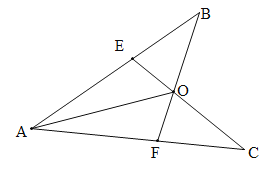
(1)∠B=∠C
(2)AO平分∠BAC
【答案】(1)答案见解析;(2)答案见解析
【解析】
(1)由SAS证得△AEC≌△AFB,即可得出结论;
(2)先证△EBO≌△FCO,得出OB=OC,再由SSS证明△AOB≌△AOC,即可得出结论.
(1)在△AEC与△AFB中,∵AE=AF,∠EAF=∠EAF,AC=AB,∴△AEC≌△AFB(SAS),∴∠C=∠B;
(2)∵AB=AC,AE=AF,∴BE=CF.
在△BEO和△CFO中,∵∠B=∠C,∠EOB=∠FOC,BE=CF,∴△BEO≌△CFO,∴BO=CO.
在△AOB和△AOC中,∵AB=AC,AO=AO,OB=OC,∴△AOB≌△AOC,∴∠BAO=∠CAO,∴AO平分∠BAC.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:初中数学 来源: 题型:
【题目】探究下面的问题:
(1)如图甲,在边长为a的正方形中去掉一个边长为b的小正方形(a>b),把余下的部分剪拼成如图乙的一个长方形,通过计算两个图形(阴影部分)的面积,验证了一个等式,这个等式是________(用式子表示),即乘法公式中的___________公式.
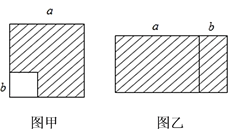
(2)运用你所得到的公式计算:
①10.7×9.3
②![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
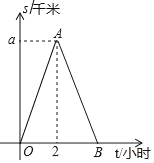
【题目】小明从家出发沿滨江路到外滩公园徒步锻炼,到外滩公园后立即沿原路返回,小明离开家的路程s(单位:千米)与走步时间t(单位:小时)之间的函数关系如图所示,其中从家到外滩公园的平均速度是4千米/时,根据图形提供的信息,解答下列问题:
(1)求图中的a值;
(2)若在距离小明家5千米处有一个地点C,小明从第一层经过点C到第二层经过点C,所用时间为1.75小时,求小明返回过程中,s与t的函数解析式,不必写出自变量的取值范围;
(3)在(2)的条件下,求小明从出发到回到家所用的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
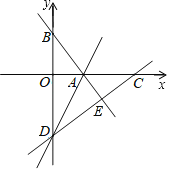
【题目】如图,在平面直角坐标系中,直线AB与x轴、y轴分别交于点A(3,0)、B(0,4),点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
(1)求直线AB的表达式;
(2)求点C和点D的坐标;
(3)y轴的正半轴上是否存在一点P,使得S△PAB=![]() S△OCD?若存在,求出点P的坐标;若不存在,请说明理由.
S△OCD?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收贵的价目表如下(注:水费按月份结算,![]() 表示立方米)
表示立方米)
价目表 | |
每月用水量 | 价格 |
不超过 |
|
超出 |
|
超出 |
|
![]() 某户居民1月份和2月份的用水量分别为
某户居民1月份和2月份的用水量分别为![]() 和
和![]() ,则应收水费分别是 元和 元
,则应收水费分别是 元和 元
![]() 若该户居民
若该户居民![]() 月份用水量
月份用水量![]() (其中
(其中![]() ),则应收水费多少元? (用含
),则应收水费多少元? (用含![]() 的式子表示,并化简)
的式子表示,并化简)
![]() 若该户居民
若该户居民![]() 两个月共用水
两个月共用水 ![]() (
(![]() 月份用水量超过
月份用水量超过![]() 月份),设
月份),设![]() 月份用水
月份用水![]() ,求该户居民
,求该户居民![]() 两个月共交水费多少元? (用含
两个月共交水费多少元? (用含 ![]() 的式子表示,并化简)
的式子表示,并化简)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 分别是数轴上四个整数所对应的点,其中有一点是原点,并且这四个整数点每相邻两点之间的距离为1个单位长度.数
分别是数轴上四个整数所对应的点,其中有一点是原点,并且这四个整数点每相邻两点之间的距离为1个单位长度.数![]() 对应的点在
对应的点在![]() 与
与![]() 之间,数
之间,数![]() 对应的点在
对应的点在![]() 与
与![]() 之间.若
之间.若![]() ,则原点是( )
,则原点是( )
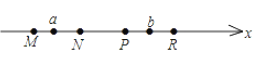
A.![]() 或
或![]() B.
B.![]() 与
与![]() C.
C.![]() 与
与![]() D.
D.![]() 与
与![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
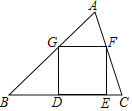
【题目】如图,已知正方形DEFG的顶点D、E在△ABC的边BC上,顶点G、F分别在边AB、AC上.如果BC=4,△ABC的面积是6,那么这个正方形的边长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD与四边形CEFG是两个正方形,边长分别为a,b,其中B,C,E在一条直线上,G在线段CD上,三角形AGE的面积为S.
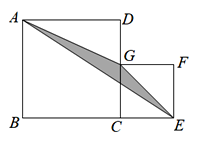
(1)①当a=5,b=3时,求S的值;
②当a=7,b=3时,求S的值;
(2)从以上结果中,请你猜想S与a,b中的哪个量有关?用字母a,b表示S,并对你的猜想进行证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com