
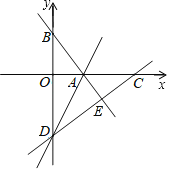
【题目】如图,在平面直角坐标系中,直线AB与x轴、y轴分别交于点A(3,0)、B(0,4),点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
(1)求直线AB的表达式;
(2)求点C和点D的坐标;
(3)y轴的正半轴上是否存在一点P,使得S△PAB=![]() S△OCD?若存在,求出点P的坐标;若不存在,请说明理由.
S△OCD?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】(1)y=﹣![]() x+4;(2)C(8,0),D(0,-6);(3)存在,P(0,8)
x+4;(2)C(8,0),D(0,-6);(3)存在,P(0,8)
【解析】
(1)将点A、B的坐标代入一次函数表达式:y=kx+b,即可求解;
(2)由题意得:AD=AB=5,故点D(8,0),设点C的坐标为:(0,m),而CD=BC,即4﹣m=![]() ,再解答即可;
,再解答即可;
(3)设点P(0,n),![]() S△OCD=
S△OCD=![]() =
=![]() ×6×8=6,S△ABP=
×6×8=6,S△ABP=![]() BP×xA=
BP×xA=![]() |4﹣m|×3=6,即可求解.
|4﹣m|×3=6,即可求解.
解:(1)设直线AB的表达式为:y=kx+b
将点A、B的坐标代入一次函数表达式:y=kx+b
得:![]() ,解得:
,解得: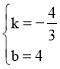 ,
,
故直线AB的表达式为:y=﹣![]() x+4;
x+4;
(2)∵AB=![]()
由折叠可得:AC=AB=5,故点C(8,0),
设点D的坐标为:(0,m),而CD=BC,
即4﹣m=![]() ,解得:m=﹣6,
,解得:m=﹣6,
故点D(0,﹣6);
(3)设点P(0,n),
∵![]() S△OCD=
S△OCD=![]() =
=![]() ×6×8=6,
×6×8=6,
∴S△ABP=![]() BP×xA=
BP×xA=![]() |4﹣n|×3=6,
|4﹣n|×3=6,
解得:n=8或0,
又∵点P在y轴的正半轴,
∴n=8,
故P(0,8).


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=108°,EF、MN分别是AB、AC的垂直平分线,点E、N在BC上,则∠EAN等于( )
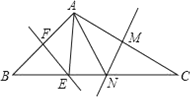
A. 72°B. 54°C. 36°D. 18°
查看答案和解析>>
科目:初中数学 来源: 题型:
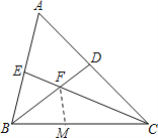
【题目】在△ABC中,∠A=60°,BD,CE是△ABC的两条角平分线,且BD,CE交于点F,如图所示,用等式表示BE,BC,CD这三条线段之间的数量关系,并证明你的结论;
晓东通过观察,实验,提出猜想:BE+CD=BC,他发现先在BC上截取BM,使BM=BE,连接FM,再利用三角形全等的判定和性质证明CM=CD即可.
(1)下面是小东证明该猜想的部分思路,请补充完整;
①在BC上截取BM,使BM=BE,连接FM,则可以证明△BEF与______全等,判定它们全等的依据是______;
②由∠A=60°,BD,CE是△ABC的两条角平分线,可以得出∠EFB=______°;
(2)请直接利用①,②已得到的结论,完成证明猜想BE+CD=BC的过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为5里,12里,13里,问这块沙田面积有多大?题中“里”是我国市制长度单位,1里=500米,则该沙田的面积为( )
A. 7.5平方千米 B. 15平方千米 C. 75平方千米 D. 750平方千米
查看答案和解析>>
科目:初中数学 来源: 题型:
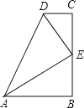
【题目】在数学活动课上,小明提出这样一个问题:∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CDE=55°.如图,则∠EAB的度数为_________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,E是边CD上一点(点E不与点C、D重合),连结BE.
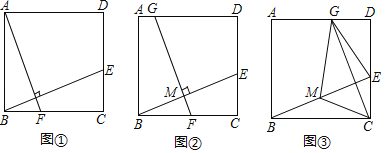
(感知)如图①,过点A作AF⊥BE交BC于点F.易证△ABF≌△BCE.(不需要证明)
(探究)如图②,取BE的中点M,过点M作FG⊥BE交BC于点F,交AD于点G.
(1)求证:BE=FG.
(2)连结CM,若CM=1,则FG的长为 .
(应用)如图③,取BE的中点M,连结CM.过点C作CG⊥BE交AD于点G,连结EG、MG.若CM=3,则四边形GMCE的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点![]() 若点D为BC边的中点,点M为线段EF上一动点,则
若点D为BC边的中点,点M为线段EF上一动点,则![]() 周长的最小值为
周长的最小值为![]()
![]()

A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com