
����Ŀ��ǽ�϶�����һ������Χ�ɵ�������״�������ͼʵ����ʾ����λ��cm����Сӱ�������µĶ���ȥ��������������������һ�������Σ���ͼ������ʾ��Сӱ���������εij�������Ϊ�������ף�����賤���εij�Ϊxcm���������⣬�ɵ÷���Ϊ��������
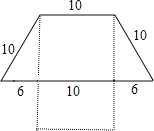
A.2��x+10����10��4+6��2B.2��x+10����10��3+6��2
C.2x+10��10��4+6��2D.2��x+10����10��2+6��2

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������ֵ��֪ʶ�ش��������⣺
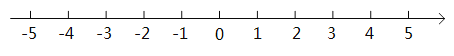
��1��̽����
�������ϱ�ʾ![]() ��
��![]() ������֮��ľ����� ��
������֮��ľ����� ��
�������ϱ�ʾ![]() ��
��![]() ������֮��ľ����� ��
������֮��ľ����� ��
�������ϱ�ʾ![]() ��
��![]() ������֮��ľ����� ��
������֮��ľ����� ��
��2�����ɣ�
һ��ģ������ϱ�ʾ��m����n������֮��ľ������ .
��3��Ӧ�ã�
�������ʾ��![]() ��3������֮��ľ�����9����ɼ�Ϊ��
��3������֮��ľ�����9����ɼ�Ϊ��![]() ����ô
����ô![]() .
.
���������ϱ�ʾ��![]() �ĵ�λ��
�ĵ�λ��![]() ��
��![]() ֮�䣬��
֮�䣬��![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����С�����̵�ÿ����ÿƿ3Ԫ�ļ۸���̳������������̣�Ȼ����ÿƿ6Ԫ�ļ۸���ۣ�������������꣬ʣ���ֻ�е�����������¼��30���������������λ��ƿ�����������±���
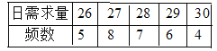
��1������30��������������������
��2���������̵�����30����ÿ�칺��28ƿ������30���������λ��Ԫ����ƽ������
��3����30��¼�ĸ���������Ƶ����Ϊ�������Ƿ����ĸ��ʣ������̵�ÿ�칺��28ƿ���������¼��30������������81Ԫ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��̽�����������:
(1)��ͼ�ף��ڱ߳�Ϊa����������ȥ��һ���߳�Ϊb��С������(a��b)�������µIJ��ּ�ƴ����ͼ�ҵ�һ�������Σ�ͨ����������ͼ��(��Ӱ����)���������֤��һ����ʽ�������ʽ��________(��ʽ�ӱ�ʾ)�����˷���ʽ�е�___________��ʽ.
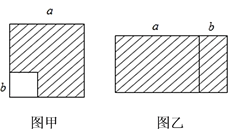
(2)���������õ��Ĺ�ʽ���㣺
��10.7��9.3
��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
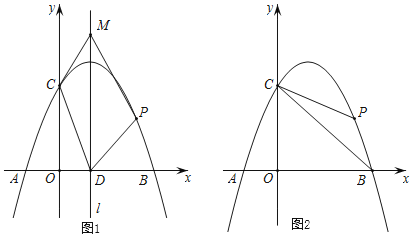
����Ŀ����ͼ1����֪������y=��x2+bx+c��x�ύ��A����1��0����B��3��0�����㣬��y�ύ��C�㣬��P�����������ڵ�һ�����ڵ�һ�����㣬�ҵ�P�ĺ�����Ϊt��
��1���������ߵı���ʽ��
��2���������ߵĶԳ���Ϊl��l��x��Ľ���ΪD����ֱ��l���Ƿ���ڵ�M��ʹ���ı���CDPM��ƽ���ı��Σ������ڣ������M�����ꣻ�������ڣ���˵�����ɣ�
��3����ͼ2������BC��PB��PC������PBC�����ΪS��
����S����t�ĺ�������ʽ��
����P�㵽ֱ��BC�ľ�������ֵ���������ʱ��P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
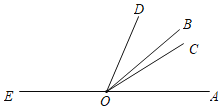
����Ŀ����ͼ����O��ֱ��AE�ϵ�һ�㣬OC�ǡ�AOD��ƽ���ߣ���BOD��![]() ��AOD��
��AOD��
��1������BOD��20�������BOC�Ķ�����
��2������BOC��n�����ú���n�Ĵ���ʽ��ʾ��EOD�Ĵ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������y=![]() ��kΪ��������k��0����ͼ����A��1��3����B��3��m����
��kΪ��������k��0����ͼ����A��1��3����B��3��m����
��1�����������Ľ���ʽ��B������ꣻ
��2����x������һ��P��ʹPA+PB��ֵ��С�������������ĵ�P�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
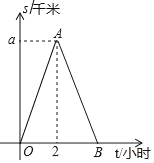
����Ŀ��С���Ӽҳ����ر���·����̲��ͽ������������̲����������ԭ·���أ�С���뿪�ҵ�·��s����λ��ǧ�ף����߲�ʱ��t����λ��Сʱ��֮��ĺ�����ϵ��ͼ��ʾ�����дӼҵ���̲����ƽ���ٶ���4ǧ��/ʱ������ͼ���ṩ����Ϣ������������⣺
��1����ͼ�е�aֵ��
��2�����ھ���С����5ǧ�״���һ���ص�C��С���ӵ�һ�㾭����C���ڶ��㾭����C������ʱ��Ϊ1.75Сʱ����С�����ع����У�s��t�ĺ�������ʽ������д���Ա�����ȡֵ��Χ��
��3���ڣ�2���������£���С���ӳ������ص������õ�ʱ�䣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
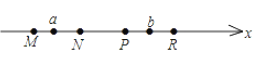
����Ŀ����ͼ��![]() �ֱ����������ĸ���������Ӧ�ĵ㣬������һ����ԭ�㣬�������ĸ�������ÿ��������֮��ľ���Ϊ1����λ���ȣ���
�ֱ����������ĸ���������Ӧ�ĵ㣬������һ����ԭ�㣬�������ĸ�������ÿ��������֮��ľ���Ϊ1����λ���ȣ���![]() ��Ӧ�ĵ���
��Ӧ�ĵ���![]() ��
��![]() ֮�䣬��
֮�䣬��![]() ��Ӧ�ĵ���
��Ӧ�ĵ���![]() ��
��![]() ֮�䣮��
֮�䣮��![]() ����ԭ���ǣ� ��
����ԭ���ǣ� ��
A.![]() ��
��![]() B.
B.![]() ��
��![]() C.
C.![]() ��
��![]() D.
D.![]() ��
��![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com