
【题目】结合数轴与绝对值的知识回答下列问题:
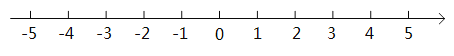
(1)探究:
①数轴上表示![]() 和
和![]() 的两点之间的距离是 ;
的两点之间的距离是 ;
②数轴上表示![]() 和
和![]() 的两点之间的距离是 ;
的两点之间的距离是 ;
③数轴上表示![]() 和
和![]() 的两点之间的距离是 ;
的两点之间的距离是 ;
(2)归纳:
一般的,数轴上表示数m与数n的两点之间的距离等于 .
(3)应用:
①如果表示数![]() 和3的两点之间的距离是9,则可记为:
和3的两点之间的距离是9,则可记为:![]() ,那么
,那么![]() .
.
②若数轴上表示数![]() 的点位于
的点位于![]() 与
与![]() 之间,求
之间,求![]() 的值.
的值.
【答案】(1)3,6,7;(2)![]() ;(3)①12或-6;②9.
;(3)①12或-6;②9.
【解析】
(1)根据数轴上点坐标的意义,可得答案;
(2)由(1)的计算即可得出规律.
(3)①根据数轴上到3距离等于9的点有12和-6,即可解答;
②根据绝对值的性质去掉绝对值号,然后计算即可得解.
解:(1)探究:①数轴上表示4和1的两点之间的距离是![]() ,②数轴上表示
,②数轴上表示![]() 和
和![]() 的两点之间的距离=
的两点之间的距离=![]() ,③数轴上表示
,③数轴上表示![]() 和5的两点之间的距离=
和5的两点之间的距离=![]() ,
,
故答案为:3,6,7.
(2)由(1)可知数轴上表示数m与数n的两点之间的距离=![]() ,
,
故答案为:![]() .
.
(3)①如果表示数![]() 和3的两点之间的距离是9,则可记为:
和3的两点之间的距离是9,则可记为:![]() ,那么
,那么![]() 或
或![]() ,
,
故答案为:12或![]() ;
;
②若数轴上表示数![]() 的点位于
的点位于![]() 与5之间,则
与5之间,则![]() ,
,
![]() ;
;


科目:初中数学 来源: 题型:
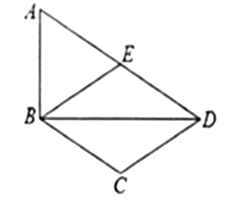
【题目】如图,在四边形ABCD中,BD为一条对角线,![]() 且
且![]() ,
,![]() ,E为AD的中点,连接BE.
,E为AD的中点,连接BE.
(1)求证:四边形BCDE为菱形;
(2)连接AC,若AC平分![]() ,
,![]() ,求AC的长.
,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
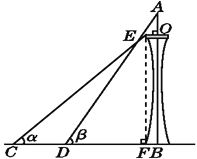
【题目】如图,某塔观光层的最外沿点E为蹦极项目的起跳点.已知点E离塔的中轴线AB的距离OE为10米,塔高AB为123米(AB垂直地面BC),在地面C处测得点E的仰角α=45°,从点C沿CB方向前行40米到达D点,在D处测得塔尖A的仰角β=60°,求点E离地面的高度EF.(结果精确到0.1米)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小刚相约周末到雪莲大剧院看演出,他们的家分别距离剧院1200m和2000m,两人分别从家中同时出发,已知小明和小刚的速度比是3:4,结果小明比小刚提前4min到达剧院.求两人的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
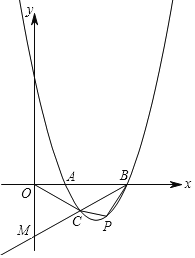
【题目】如图,抛物线y=a(x﹣1)(x﹣3)(a>0)与x轴交于A、B两点,抛物线上另有一点C在x轴下方,且使△OCA∽△OBC.
(1)求线段OC的长度;
(2)设直线BC与y轴交于点M,点C是BM的中点时,求直线BM和抛物线的解析式;
(3)在(2)的条件下,直线BC下方抛物线上是否存在一点P,使得四边形ABPC面积最大?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
已知![]() ,
,![]() ,
,![]() ,…
,…![]() 都是不等于0的有理数,若
都是不等于0的有理数,若![]() ,求
,求![]() 的值.
的值.
解:当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,所以
,所以![]() 参照以上解答,试探究以下问题:
参照以上解答,试探究以下问题:
(1)若![]() ,求
,求![]() 的值
的值
(2)若![]() ,则
,则![]() 的值为__________;
的值为__________;
(3)由(1)、(2)试猜想,![]() 共有__________个不同的值,在
共有__________个不同的值,在![]() 这些不同的值中,最大的值和最小的值的差等于__________.
这些不同的值中,最大的值和最小的值的差等于__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个大小不同的等腰直角三角板如图1所示放置,图2是由它抽象出的几何图形,图中AB=AC,AD=AE,∠BAC=∠EAD=90°,B,C,E在同一条直线上,连结DC.
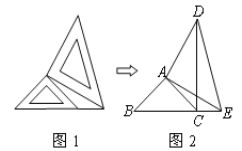
(1)图2中的全等三角形是_______________,并给予证明(说明:结论中不得含有未标识的字母);
(2)指出线段DC和线段BE的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】墙上钉着用一根彩绳围成的梯形形状的饰物,如图实线所示(单位:cm).小颖将梯形下底的钉子去掉,并将这条彩绳钉成一个长方形,如图虚线所示.小颖所钉长方形的长、宽各为多少厘米?如果设长方形的长为xcm,根据题意,可得方程为( )
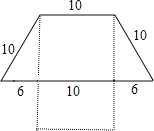
A.2(x+10)=10×4+6×2B.2(x+10)=10×3+6×2
C.2x+10=10×4+6×2D.2(x+10)=10×2+6×2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com