
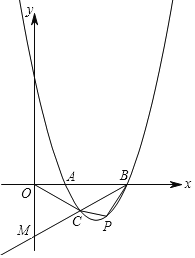
【题目】如图,抛物线y=a(x﹣1)(x﹣3)(a>0)与x轴交于A、B两点,抛物线上另有一点C在x轴下方,且使△OCA∽△OBC.
(1)求线段OC的长度;
(2)设直线BC与y轴交于点M,点C是BM的中点时,求直线BM和抛物线的解析式;
(3)在(2)的条件下,直线BC下方抛物线上是否存在一点P,使得四边形ABPC面积最大?若存在,请求出点P的坐标;若不存在,请说明理由.
【答案】(1)OC=![]() ;(2)y=
;(2)y=![]() x﹣
x﹣![]() ,抛物线解析式为y=
,抛物线解析式为y=![]() x2﹣
x2﹣![]() x+2
x+2![]() ;(3)点P存在,坐标为(
;(3)点P存在,坐标为(![]() ,﹣
,﹣![]() ).
).
【解析】
(1)令y=0,求出x的值,确定出A与B坐标,根据已知相似三角形得比例,求出OC的长即可;
(2)根据C为BM的中点,利用直角三角形斜边上的中线等于斜边的一半得到OC=BC,确定出C的坐标,利用待定系数法确定出直线BC解析式,把C坐标代入抛物线求出a的值,确定出二次函数解析式即可;
(3)过P作x轴的垂线,交BM于点Q,设出P与Q的横坐标为x,分别代入抛物线与直线解析式,表示出坐标轴,相减表示出PQ,四边形ACPB面积最大即为三角形BCP面积最大,三角形BCP面积等于PQ与B和C横坐标之差乘积的一半,构造为二次函数,利用二次函数性质求出此时P的坐标即可.
(1)由题可知当y=0时,a(x﹣1)(x﹣3)=0,
解得:x1=1,x2=3,即A(1,0),B(3,0),
∴OA=1,OB=3
∵△OCA∽△OBC,
∴OC:OB=OA:OC,
∴OC2=OAOB=3,
则OC=![]() ;
;
(2)∵C是BM的中点,即OC为斜边BM的中线,
∴OC=BC,
∴点C的横坐标为![]() ,
,
又OC=![]() ,点C在x轴下方,
,点C在x轴下方,
∴C(![]() ,﹣
,﹣![]() ),
),
设直线BM的解析式为y=kx+b,
把点B(3,0),C(![]() ,﹣
,﹣![]() )代入得:
)代入得: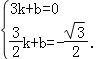 ,
,
解得:b=﹣![]() ,k=
,k=![]() ,
,
∴y=![]() x﹣
x﹣,
又∵点C(![]() ,﹣
,﹣![]() )在抛物线上,代入抛物线解析式,
)在抛物线上,代入抛物线解析式,
解得:a=![]() ,
,
∴抛物线解析式为y=![]() x2﹣
x2﹣![]() x+2
x+2![]() ;
;
(3)点P存在,
设点P坐标为(x,![]() x2﹣
x2﹣![]() x+2
x+2![]() ),过点P作PQ⊥x轴交直线BM于点Q,
),过点P作PQ⊥x轴交直线BM于点Q,
则Q(x,![]() x﹣
x﹣![]() ),
),
∴PQ=![]() x﹣
x﹣![]() ﹣(
﹣(![]() x2﹣
x2﹣![]() x+2
x+2![]() )=﹣
)=﹣![]() x2+3
x2+3![]() x﹣3
x﹣3![]() ,
,
当△BCP面积最大时,四边形ABPC的面积最大,
S△BCP=![]() PQ(3﹣x)+
PQ(3﹣x)+![]() PQ(x﹣
PQ(x﹣![]() )=
)=![]() PQ=﹣
PQ=﹣![]() x2+
x2+![]() x﹣
x﹣![]() ,
,
当x=﹣![]() 时,S△BCP有最大值,四边形ABPC的面积最大,此时点P的坐标为(
时,S△BCP有最大值,四边形ABPC的面积最大,此时点P的坐标为(![]() ,﹣
,﹣![]() ).
).


科目:初中数学 来源: 题型:
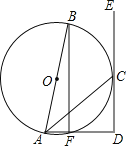
【题目】如图,AB是⊙O的直径,ED切⊙O于点C,AD交⊙O于点F,∠AC平分∠BAD,连接BF.
(1)求证:AD⊥ED;
(2)若CD=4,AF=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点G为对角线AC上一点,AG=AB.∠CAE=15°且AE=AC,连接GE.将线段AE绕点A逆时针旋转得到线段AF,使DF=GE,则∠CAF的度数为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E在△DBC的边DB上,点A在△DBC内部,∠DAE=∠BAC=90°,AD=AE,AB=AC.给出下列结论:
①BD=CE;②∠ABD+∠ECB=45°;③BD⊥CE;④BE2=2(AD2+AB2)﹣CD2.其中正确的是( )

A. ①②③④ B. ②④ C. ①②③ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的方程2x2﹣5xsinA+2=0有两个相等的实数根,其中∠A是锐角三角形ABC的一个内角.
(1)求sinA的值;
(2)若关于y的方程y2﹣10y+k2﹣4k+29=0的两个根恰好是△ABC的两边长,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】结合数轴与绝对值的知识回答下列问题:
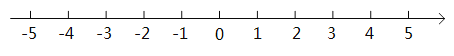
(1)探究:
①数轴上表示![]() 和
和![]() 的两点之间的距离是 ;
的两点之间的距离是 ;
②数轴上表示![]() 和
和![]() 的两点之间的距离是 ;
的两点之间的距离是 ;
③数轴上表示![]() 和
和![]() 的两点之间的距离是 ;
的两点之间的距离是 ;
(2)归纳:
一般的,数轴上表示数m与数n的两点之间的距离等于 .
(3)应用:
①如果表示数![]() 和3的两点之间的距离是9,则可记为:
和3的两点之间的距离是9,则可记为:![]() ,那么
,那么![]() .
.
②若数轴上表示数![]() 的点位于
的点位于![]() 与
与![]() 之间,求
之间,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有五张正面分别标有数字﹣2,﹣1,0,1,2的卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中随机抽取一张,记卡片上的数字为a,则使关于x的一元二次方程x2﹣2(a﹣1)x+a(a﹣3)=0有两个不相等的实数根,且以x为自变量的二次函数y=x2﹣(a2+1)x﹣a+2的图象不经过点(1,0)的概率是__.
查看答案和解析>>
科目:初中数学 来源: 题型:
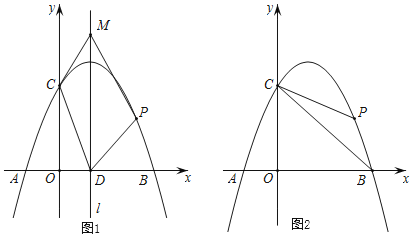
【题目】如图1,已知抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于C点,点P是抛物线上在第一象限内的一个动点,且点P的横坐标为t.
(1)求抛物线的表达式;
(2)设抛物线的对称轴为l,l与x轴的交点为D.在直线l上是否存在点M,使得四边形CDPM是平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.
(3)如图2,连接BC,PB,PC,设△PBC的面积为S.
①求S关于t的函数表达式;
②求P点到直线BC的距离的最大值,并求出此时点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com