
【题目】如图,已知正方形ABCD的边长是5,点E在DC上,将△ADE经顺时针旋转后与△ABF重合.
(1)指出旋转的中心和旋转角度;
(2)如果连接EF,那么△AEF是怎样的三角形?请说明理由;
(3)△ABF向右平移后与△DCH位置,平移的距离是多少?
(4)试猜想线段AE和DH的数量关系和位置关系,并说明理由.
【答案】
(1)解:旋转的中心是点A,旋转的角度是90°;
(2)解:△AEF是等腰直角三角形.
理由如下:
∵△ADE绕点A顺时针旋转90°后与△ABF重合,
∴∠FAE=∠BAD=90°,AF=AE,
∴△AEF是等腰直角三角形.
(3)解:∵正方形ABCD的边长是5,
∴△ABF向右平移后与△DCH位置,平移的距离是5;
(4)解:AE=DH,AE⊥DH,
理由:∵△ABF向右平移后与△DCH重合,
∴DH∥AF,DH=AF,
又∵△ADE绕着点A顺时针旋转90°后与△ABF重合,
∴∠FAE=∠BAD=90°,AF=AE,
∴AE⊥AF,
∴AE=DH,AE⊥DH.
【解析】旋转中心就是对应点连线的垂直平分线的交点,若两图形有公共点,验证一下它到对应点的距离是否相等,若相等就是旋转中心;平移距离就是对应点的距离;证垂直需根据旋转角是直角再转化.
【考点精析】解答此题的关键在于理解旋转的性质的相关知识,掌握①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在正数范围内定义运算“※”,其规则为a※b=a+b2 , 则方程x※(x+1)=5的解是( )
A.x=5
B.x=1
C.x1=1,x2=﹣4
D.x1=﹣1,x2=4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级两个班,各选派10名学生参加学校举行的“汉字听写”大赛预赛.各参赛选手的成绩如图:
九(1)班:88,91,92,93,93,93,94,98,98,100
九(2)班:89,93,93,93,95,96,96,98,98,99
通过整理,得到数据分析表如下:

(1)直接写出表中m、n的值;
(2)依据数据分析表,有人说:“最高分在(1)班,(1)班的成绩比(2)班好”,但也有人说(2)班的成绩要好,请给出两条支持九(2)班成绩好的理由;
(3)若从两班的参赛选手中选四名同学参加决赛,其中两个班的第一名直接进入决赛,另外两个名额在四个“98分”的学生中任选二个,试求另外两个决赛名额落在同一个班的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点P(﹣2,3)与点Q关于原点对称,则点Q的坐标为( )
A.(﹣2,﹣3)
B.(3,﹣2)
C.(2,3)
D.(2,﹣3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个大小不同的等腰直角三角形三角板如图①所示放置,图②是由它抽象出的几何图形,B,C,E在同一条直线上,连接DC, 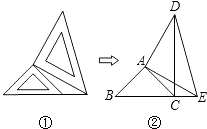
(1)请找出图②中的全等三角形,并给予说明(说明:结论中不得含有未标识的字母);
(2)试说明:DC⊥BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=2(x﹣3)2+2图象向左平移6个单位,再向下平移2个单位后,所得图象的函数表达式是( )
A.y=2(x-9)2B.y=2(x+3)2
C.y=2(x+3)2+4D.y=2(x-9)2+4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列4个三角形中,均有AB=AC,则经过三角形的一个顶点的一条直线能够将这个三角形分成两个小等腰三角形的是( ) 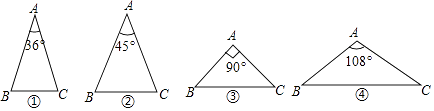
A.①③
B.①②④
C.①③④
D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法不正确的是( )
A. 过任意一点可作已知直线的一条平行线
B. 同一平面内两条不相交的直线是平行线
C. 在同一平面内,过一点只能画一条直线与已知直线垂直
D. 在同一平面内,经过直线外一点有且只有一条直线与已知直线平行
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com