
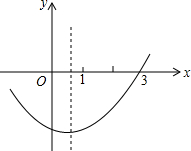
 如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,现有下列结论:①abc<0;②b2-4ac+5>0;③2a+b<0;④a-b+c<0;⑤抛物线y=ax2+bx+c(a≠0)与x轴的另一个点坐标为(-1,0),其中正确的是②④(把所有正确结论的序号都填在横线上)
如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,现有下列结论:①abc<0;②b2-4ac+5>0;③2a+b<0;④a-b+c<0;⑤抛物线y=ax2+bx+c(a≠0)与x轴的另一个点坐标为(-1,0),其中正确的是②④(把所有正确结论的序号都填在横线上) 分析 由抛物线的开口方向可确定a的符号,由抛物线的对称轴相对于y轴的位置可得a与b之间的符号关系,由抛物线与y轴的交点位置可确定c的符号;由抛物线与x轴交点个数可确定b2-4ac的符号;根据抛物线的对称轴与x=1的大小关系可推出2a+b的符号;根据抛物线的对称性即可知道抛物线与x轴的左交点位置;由于x=-1时y=a-b+c,因而结合图象,可根据x=-1时y的符号来确定a-b+c的符号.
解答 解:由抛物线的开口向上可得a>0,
由抛物线的对称轴在y轴的右边可得x=-$\frac{b}{2a}$>0,则a与b异号,因而b<0,
由抛物线与y轴的交点在y轴的负半轴上可得c<0,
∴abc>0,故①错误;
由抛物线与x轴有两个交点可得b2-4ac>0,因而b2-4ac+5>0,故②正确;
由抛物线的对称轴x=-$\frac{b}{2a}$<1(a>0),可得-b<2a,即2a+b>0,故③错误;
设抛物线与x轴的左交点为(m,0),根据对称性可得: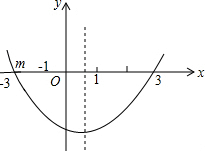
抛物线的对称轴x=$\frac{m+3}{2}$.
由图可知0<$\frac{m+3}{2}$<1,
解得-3<m<-1.
因而抛物线与x轴的另一个交点坐标不是(-1,0),故⑤错误;
当x=-1时y<0,即a-b+c<0,故④正确;
综上所述:②、④正确.
故答案为②、④.
点评 本题主要考查二次函数图象与系数的关系,其中a决定于抛物线的开口方向,b决定于抛物线的开口方向及抛物线的对称轴相对于y轴的位置,c决定于抛物线与y轴的交点位置,b2-4ac的符号决定于抛物线与x轴交点个数,2a+b的符号决定于a的符号及-$\frac{b}{2a}$与1的大小关系,运用数形结合的思想准确获取相关信息是解决本题的关键.


 能力评价系列答案
能力评价系列答案科目:初中数学 来源: 题型:解答题
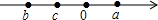 “数形结合”是一种重要的数字方法.如在化简|a|时,当a在数轴上位于原点的右侧时,|a|=a;当a在数轴上位于原点时,|a|=0;当a在数轴上位原点的左侧时,|a|=-a.试用这种方法解决下列问题.
“数形结合”是一种重要的数字方法.如在化简|a|时,当a在数轴上位于原点的右侧时,|a|=a;当a在数轴上位于原点时,|a|=0;当a在数轴上位原点的左侧时,|a|=-a.试用这种方法解决下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
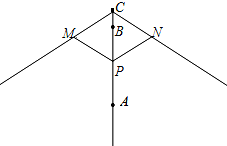 如图为太阳伞示意图,当伞收紧时,点P与点A重合,当伞慢慢撑开时,动点P由A向B移动;当点P到过点B时,伞张得最开.已知伞在撑开的过程中,总有PM=PN=CM=CN.则下列说法错误的是( )
如图为太阳伞示意图,当伞收紧时,点P与点A重合,当伞慢慢撑开时,动点P由A向B移动;当点P到过点B时,伞张得最开.已知伞在撑开的过程中,总有PM=PN=CM=CN.则下列说法错误的是( )| A. | 四边形PNCM可能会出现为正方形 | B. | 四边形PNCM的周长始终不变 | ||
| C. | 当∠CPN=60°时,CP=AP | D. | 四边形PNCM的面积始终不变 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
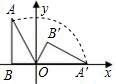 如图,在Rt△ABO中,∠B=90°,∠A=30°,OB=2,现将Rt△ABO在坐标平面内绕原点O按顺时针方向旋转到△OA′B′的位置.求:
如图,在Rt△ABO中,∠B=90°,∠A=30°,OB=2,现将Rt△ABO在坐标平面内绕原点O按顺时针方向旋转到△OA′B′的位置.求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com