
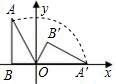
 如图,在Rt△ABO中,∠B=90°,∠A=30°,OB=2,现将Rt△ABO在坐标平面内绕原点O按顺时针方向旋转到△OA′B′的位置.求:
如图,在Rt△ABO中,∠B=90°,∠A=30°,OB=2,现将Rt△ABO在坐标平面内绕原点O按顺时针方向旋转到△OA′B′的位置.求:分析 (1)作B′C⊥x轴于C,如图,根据旋转的性质得∠A′OB′=∠AOB=60°,OB′=OB=2,然后在Rt△OB′C中,利用含30度的直角三角形三边的关系求出OC,B′C,则可得到点B′的坐标;
(2)先计算OA的长和∠AOA′的度数,然后根据弧长公式计算;
(3)根据扇形面积公式计算.
解答 解:(1)作B′C⊥x轴于C,如图, 在Rt△ABO中,
在Rt△ABO中,
∵∠B=90°,∠A=30°,OB=2,
∴∠AOB=60°,
∵Rt△ABO绕原点O按顺时针方向旋转到△OA′B′,
∴∠A′OB′=∠AOB=60°,OB′=OB=2,
在Rt△OB′C中,∵∠OB′C=30°,
∴OC=$\frac{1}{2}$OB′=1,B′C=$\sqrt{3}$OC=$\sqrt{3}$,
∴点B′的坐标为(1,$\sqrt{3}$);
(2)∵∠B=90°,∠A=30°,OB=2,
∴OA=2OB=4,
∵∠AOA′=120°,
∴顶点A从开始到点A′结束经过的路径长=$\frac{120•π•4}{180}$=$\frac{8}{3}$π;
(3)扇形AOA′的面积=$\frac{1}{2}$•$\frac{8}{3}$π•4=$\frac{16}{3}$π.
点评 本题考查了坐标与图形变化-旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
 如图,点D为等腰直角三角形ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.
如图,点D为等腰直角三角形ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
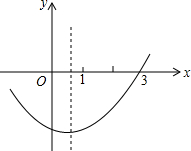 如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,现有下列结论:①abc<0;②b2-4ac+5>0;③2a+b<0;④a-b+c<0;⑤抛物线y=ax2+bx+c(a≠0)与x轴的另一个点坐标为(-1,0),其中正确的是②④(把所有正确结论的序号都填在横线上)
如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,现有下列结论:①abc<0;②b2-4ac+5>0;③2a+b<0;④a-b+c<0;⑤抛物线y=ax2+bx+c(a≠0)与x轴的另一个点坐标为(-1,0),其中正确的是②④(把所有正确结论的序号都填在横线上)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
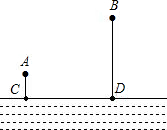 如图,A、B两个村子在河边CD的同侧,A、B两村到河边的距离分别为AC=1千米,BD=3千米,CD=3千米.现在河边CD建一座水厂,建成后的水厂,可以直接向A、B两村送水,也可以先将水送一村再转送至另一村.铺设水管费用为每千米2万元,试在河边CD选择水厂位置确定方案,使铺设水管费用最省.并求出铺设水管的总费用(精确到0.01万元).
如图,A、B两个村子在河边CD的同侧,A、B两村到河边的距离分别为AC=1千米,BD=3千米,CD=3千米.现在河边CD建一座水厂,建成后的水厂,可以直接向A、B两村送水,也可以先将水送一村再转送至另一村.铺设水管费用为每千米2万元,试在河边CD选择水厂位置确定方案,使铺设水管费用最省.并求出铺设水管的总费用(精确到0.01万元).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
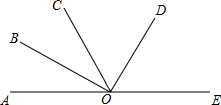 如图所示,O是直线AE上的-点,OB是∠AOC的平分线,OD是∠COE的平分线.
如图所示,O是直线AE上的-点,OB是∠AOC的平分线,OD是∠COE的平分线.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com