
分析 根据正比例函数和反比例函数的定义设y1=mx,y2=$\frac{n}{x}$,则y=mx+$\frac{n}{x}$,再把两组对应值代入得到关于m、n的方程组,然后解方程组求出m、n即可.
解答 解:解:设y1=mx,y2=$\frac{n}{x}$,
则y=mx+$\frac{n}{x}$,
根据题意得$\left\{\begin{array}{l}{3m+\frac{n}{3}=4}\\{m+n=2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=\frac{5}{4}}\\{n=\frac{3}{4}}\end{array}\right.$.
所以y与x的函数表达式为y=$\frac{5}{4}$x+$\frac{3}{4x}$.
点评 本题考查了待定系数法求反比例函数的解析式:(1)设出含有待定系数的反比例函数解析式y=$\frac{k}{x}$(k为常数,k≠0);(2)把已知条件(自变量与函数的对应值)代入解析式,得到待定系数的方程;(3)解方程,求出待定系数;(4)写出解析式.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:解答题
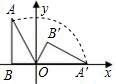 如图,在Rt△ABO中,∠B=90°,∠A=30°,OB=2,现将Rt△ABO在坐标平面内绕原点O按顺时针方向旋转到△OA′B′的位置.求:
如图,在Rt△ABO中,∠B=90°,∠A=30°,OB=2,现将Rt△ABO在坐标平面内绕原点O按顺时针方向旋转到△OA′B′的位置.求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com