
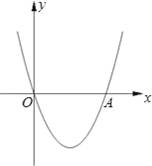
如图,在直角坐标系xOy中,二次函数y=x2+(2k﹣1)x+k+1的图象与x轴相交于O、A两点.
(1)求这个二次函数的解析式;
(2)在这条抛物线的对称轴右边的图象上有一点B,使△AOB的面积等于6,求点B的坐标;
(3)对于(2)中的点B,在此抛物线上是否存在点P,使∠POB=90°?若存在,求出点P的坐标,并求出△POB的面积;若不存在,请说明理由.

【考点】二次函数综合题.
【专题】压轴题.
【分析】(1)将原点坐标代入抛物线中即可求出k的值,也就得出了抛物线的解析式.
(2)根据(1)得出的抛物线的解析式可得出A点的坐标,也就求出了OA的长,根据△OAB的面积可求出B点纵坐标的绝对值,然后将符合题意的B点纵坐标代入抛物线的解析式中即可求出B点的坐标,然后根据B点在抛物线对称轴的右边来判断得出的B点是否符合要求即可.
(3)根据B点坐标可求出直线OB的解析式,由于OB⊥OP,由此可求出P点的坐标特点,代入二次函数解析式可得出P点的坐标.求△POB的面积时,可先求出OB,OP的长度即可求出△BOP的面积.
【解答】解:①∵函数的图象与x轴相交于O,
∴0=k+1,
∴k=﹣1,
∴y=x2﹣3x,
②假设存在点B,过点B做BD⊥x轴于点D,
∵△AOB的面积等于6,
∴
 AO•BD=6,
AO•BD=6,
当0=x2﹣3x,
x(x﹣3)=0,
解得:x=0或3,
∴AO=3,
∴BD=4
即4=x2﹣3x,
解得:x=4或x=﹣1(舍去).
又∵顶点坐标为:( 1.5,﹣2.25).
∵2.25<4,
∴x轴下方不存在B点,
∴点B的坐标为:(4,4);
③∵点B的坐标为:(4,4),
∴∠BOD=45°,BO=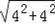
 =4
=4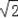
 ,
,
当∠POB=90°,
∴∠POD=45°,
设P点横坐标为:x,则纵坐标为:x2﹣3x,
即﹣x=x2﹣3x,
解得x=2 或x=0,
∴在抛物线上仅存在一点P (2,﹣2).
∴OP=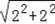
 =2
=2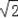
 ,
,
使∠POB=90°,
∴△POB的面积为:
 PO•BO=
PO•BO=
 ×4
×4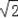
 ×2
×2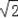
 =8.
=8.


【点评】本题考查了二次函数解析式的确定、函数图象交点、图象面积求法等知识.利用已知进行分类讨论得出符合要求点的坐标是解题关键.


科目:初中数学 来源: 题型:
鼓楼商场搞换季促销活动,若每件羽绒服按标价的5折销售可赚50元 ,按标价的6折销售可赚80元,__________________
,按标价的6折销售可赚80元,__________________ _?(请你在横线上提出一个问题然后再解答).
_?(请你在横线上提出一个问题然后再解答).
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,△ABC中,∠ACB=90°,∠A=30°,AB=16.点P是斜边AB上一点.过点P作PQ⊥AB,垂足为P,交边AC(或边CB)于点Q,设AP=x,△APQ的面积为y,则y与x之间的函数图象大致为( )
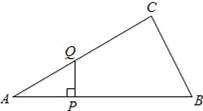

A.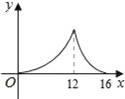
 B.
B.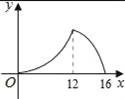
 C.
C.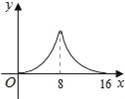
 D.
D.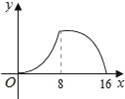

查看答案和解析>>
科目:初中数学 来源: 题型:
某校初三(1)班50名学生需要参加体育“五选一”自选项目测试,班上学生所报自选项目的情况统计表如下:
| 自选项目 | 人数 | 频率 |
| 立定跳远 | 9 | 0.18 |
| 三级蛙跳 | 12 | a |
| 一分钟跳绳 | 8 | 0.16 |
| 投掷实心球 | b | 0.32 |
| 推铅球 | 5 | 0.10 |
| 合计 | 50 | 1 |
(1)求a,b的值;
(2)若将各自选项目的人数所占比例绘制成扇形统计图,求“一分钟跳绳”对应扇形的圆心角的度数;
(3)在选报“推铅球”的学生中,有3名男生,2名女生,为了了解学生的训练效果,从这5名学生中随机抽取两名学生进行推铅球测试,求所抽取的两名学生中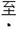

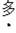
 有一名女生的概率.
有一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,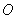 是坐标原点,菱形
是坐标原点,菱形 的顶点
的顶点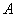 的坐标为(-3,4),顶点
的坐标为(-3,4),顶点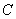 在
在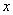 轴的负半轴上,函数
轴的负半轴上,函数 的图像经过顶点
的图像经过顶点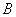 ,则
,则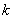 的值为 ( )
的值为 ( )
A.一12 B.一27 C.一32 D.一36
查看答案和解析>>
科目:初中数学 来源: 题型:
2015年5月17日是第25个全国助残日,今年全国助残日的主题是“关注孤独症儿童,走向美好未来”.第二次全国残疾人抽样调查结果显示,我国0~6岁精神残疾儿童约为11.1万人.11.1万用科学记数法表示为( )
A.1.11×104 B.11.1×104 C.1.11×105 D.1.11×106
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com