
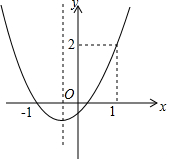
 已知抛物线y=ax2+bx+c的图象如图所示,则下列结论:
已知抛物线y=ax2+bx+c的图象如图所示,则下列结论:| A. | ①② | B. | ②③ | C. | ③④ | D. | ②④ |
分析 由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答 解:①∵抛物线的开口向上,∴a>0,
∵与y轴的交点为在y轴的负半轴上,∴c<0,
∵对称轴为x=$\frac{b}{2a}$<0,∴a、b同号,即b>0,
∴abc<0,
故本选项错误;
②当x=1时,函数值为2,
∴a+b+c=2;
故本选项正确;
③当x=-1时,函数值<0,
即a-b+c<0,(1)
又a+b+c=2,
将a+c=2-b代入(1),
2-2b<0,
∴b>1
故本选项正确;
④∵对称轴x=$-\frac{b}{2a}$>-1,
解得:$\frac{b}{2}$<a,
∵b>1,
∴a>$\frac{1}{2}$,
故本选项错误;
综上所述,其中正确的结论是②③;
故选B.
点评 本题考查的是二次函数图象与系数的关系,关键是记住二次项系数a决定抛物线的开口方向和大小,一次项系数b和二次项系数a共同决定对称轴的位置,常数项c决定抛物线与y轴交点.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形ADBC中,∠D、∠C为直角,G、I分别是△ABC、△ABD的内心,延长AG、BG、AI、BI交四边于Q、E、P、F,如果四边形GAIB的面积为17,求六边形EAFPBQ的面积.
如图,四边形ADBC中,∠D、∠C为直角,G、I分别是△ABC、△ABD的内心,延长AG、BG、AI、BI交四边于Q、E、P、F,如果四边形GAIB的面积为17,求六边形EAFPBQ的面积.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知点E(-4,2),F(-2,-2),以O为位似中心,按比例尺1:2,把△EFO缩小,则点E的对应点E′的坐标为( )
如图,已知点E(-4,2),F(-2,-2),以O为位似中心,按比例尺1:2,把△EFO缩小,则点E的对应点E′的坐标为( )| A. | (2,-1)或(-2,1) | B. | (8,-4)或(-8,-4) | C. | (2,-1) | D. | (8,-4) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3.5×108 | B. | 3.5×109 | C. | 35×108 | D. | 0.35×109 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 方程有两个不想等的实数根 | B. | 方程不一定有实数根 | ||
| C. | 方程有两个相等的实数根 | D. | 方程没有实数根 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com