
 如图,四边形ADBC中,∠D、∠C为直角,G、I分别是△ABC、△ABD的内心,延长AG、BG、AI、BI交四边于Q、E、P、F,如果四边形GAIB的面积为17,求六边形EAFPBQ的面积.
如图,四边形ADBC中,∠D、∠C为直角,G、I分别是△ABC、△ABD的内心,延长AG、BG、AI、BI交四边于Q、E、P、F,如果四边形GAIB的面积为17,求六边形EAFPBQ的面积. 分析 如图,在线段AB上分别截取AM=AE,BN=BQ,连接GM、GN,作QH⊥BE于H,ND⊥GM于D.只要证明六边形EAFPBQ的面积=2•四边形GAIB的面积即可解决问题.
解答 解:如图,在线段AB上分别截取AM=AE,BN=BQ,连接GM、GN,作QH⊥BE于H,ND⊥GM于D.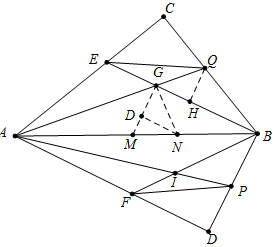
在△AGE和△AGM中,
$\left\{\begin{array}{l}{AG=AG}\\{∠GAE=∠GAM}\\{AE=AM}\end{array}\right.$,
∴△GAE≌△GAM,
∴GE=GM,∠AGE=∠AGM,
同理可证△GBQ≌△GBN,可得GQ=GN,
∵∠C=90°,∠GAB=$\frac{1}{2}$∠CAB,∠GBA=$\frac{1}{2}$∠CBA,
∴∠QCB=∠AGE=∠GAB+∠GBA=45°,
∴∠EGM=∠QGN=90°,
∴∠EGQ+∠MGN=180°,∵∠EGQ+∠QGB=180°,
∴∠QGH=∠MGN,
∵S△EGQ=$\frac{1}{2}$•EG•QG•sin∠QGH,S△MNG=$\frac{1}{2}$•GM•GN•sin∠MGN,
∴S△EGQ=S△MGN,S△AMG=S△AGE,S△GBN=S△GBQ,
∴S△ABG=S△AEG+S△EQG+S△GBQ,
同理可证S△ABI=S△AIF+S△IPF+S△BIP,
∴六边形EAFPBQ的面积=2•四边形GAIB的面积=34.
点评 本题考查三角形的内心,三角形的面积,四边形的面积,全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线构造全等三角形解决问题吗,属于中考压轴题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
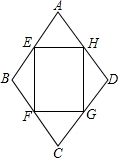 如图,四边形ABCD是一个菱形绿草地,其周长为40$\sqrt{2}$m,∠ABC=120°,在其内部有一个矩形花坛EFGH,其四个顶点恰好在菱形ABCD各边中点,现准备在花坛中种植茉莉花,其单价为30元/2,则需投资资金多少元?($\sqrt{3}$取1.732)
如图,四边形ABCD是一个菱形绿草地,其周长为40$\sqrt{2}$m,∠ABC=120°,在其内部有一个矩形花坛EFGH,其四个顶点恰好在菱形ABCD各边中点,现准备在花坛中种植茉莉花,其单价为30元/2,则需投资资金多少元?($\sqrt{3}$取1.732)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
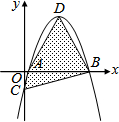 如图,坐标平面上,二次函数y=-x2+4x-k的图形与x轴交于A,B两点,与y轴交于C点,其顶点为D,且k>0,若△ABC与△ABD的面积比为1:4,则k的值为$\frac{4}{5}$.
如图,坐标平面上,二次函数y=-x2+4x-k的图形与x轴交于A,B两点,与y轴交于C点,其顶点为D,且k>0,若△ABC与△ABD的面积比为1:4,则k的值为$\frac{4}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
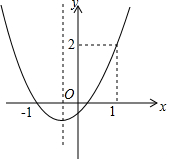 已知抛物线y=ax2+bx+c的图象如图所示,则下列结论:
已知抛物线y=ax2+bx+c的图象如图所示,则下列结论:| A. | ①② | B. | ②③ | C. | ③④ | D. | ②④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com