
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 无法确定 |
分析 过C作CD⊥AB于D,根据勾股定理求出AB,根据三角形的面积公式求出CD,得出d<r,根据直线和圆的位置关系即可得出结论.
解答 解:过C作CD⊥AB于D,如图所示: ∵在Rt△ABC中,∠C=90,AC=4,BC=3,
∵在Rt△ABC中,∠C=90,AC=4,BC=3,
∴由勾股定理得:AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵△ABC的面积=$\frac{1}{2}$AC×BC=$\frac{1}{2}$AB×CD,
∴3×4=5CD,
∴CD=2.4<2.5,
即d<r,
∴斜边AB与⊙C的位置关系是相交,
故选:A.
点评 本题考查了勾股定理,三角形的面积,直线和圆的位置关系的应用;解此题的关键是能正确作出辅助线,并进一步求出CD的长,注意:直线和圆的位置关系有:相离,相切,相交.


 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案科目:初中数学 来源: 题型:选择题
| A. | x=-$\frac{1}{2}$ | B. | x=$\frac{3}{4}$ | C. | x=$\frac{9}{4}$ | D. | x=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 方案一 | A | B | |
| 标价(单位:元) | 50 | 80 | |
| 每件商品返利 | 按标价的20% | 按标价的30% | |
| 方案二 | 若所购的A、B商品达到或超过51件(不同商品可累计),则按标价的28%返利;若没有达到51件,则不返利. | ||
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点P表示我国的钓鱼岛,在此岛周围25海里水域有暗礁.我渔政海监船由西向东航行到A处,发现P岛在北偏东60°的方向上,轮船继续向前航行20海里到达B处,发现P岛在北偏东45°的方向上.该船若不改变航向继续前进,有无触礁的危险?(参考数据$\sqrt{3}$=1.73)
如图,点P表示我国的钓鱼岛,在此岛周围25海里水域有暗礁.我渔政海监船由西向东航行到A处,发现P岛在北偏东60°的方向上,轮船继续向前航行20海里到达B处,发现P岛在北偏东45°的方向上.该船若不改变航向继续前进,有无触礁的危险?(参考数据$\sqrt{3}$=1.73)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
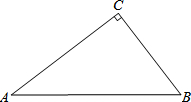 如图,△ABC中,∠A+∠B=90°.
如图,△ABC中,∠A+∠B=90°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com