
分析 (1)根据题意分别求出当2≤x≤8时,每平方米的售价应为3000-(8-x)×20元,当9≤x≤23时,每平方米的售价应为3000+(x-8)×40元;
(2)由(1)知:当2≤x≤8时,小张首付款为108000元<120000元,即可得出2~8层可任选,当9≤x≤23时,小张首付款为36(40x+2680)≤120000,9≤x≤16,即可得出小张可以购买二至十六层的任何一层.
解答 解:(1)当2≤x≤8时,每平方米的售价应为:
y=3000-(8-x)×20=20x+2840 (元/平方米),
当9≤x≤23时,每平方米的售价应为:
y=3000+(x-8)×40=40x+2680(元/平方米),
∴y=$\left\{\begin{array}{l}{20x+2840(2≤x≤8)}\\{40x+2680(9≤x≤23)}\end{array}\right.$(x为正整数);
(2)由(1)知:
当2≤x≤8时,小张首付款为
(20x+2840)×120×30%
=36(20x+2840)≤36(20×8+2840)=108000元<120000元,
∴2~8层可任选,
当9≤x≤23时,小张首付款为,
(40x+2680)×120×30%=36(40x+2680)元,
36(40x+2680)≤120000,
解得:x≤$\frac{49}{3}$,
∵x为正整数,∴9≤x≤16.
综上得:小张可以购买二至十六层的任何一层.
点评 本题考查的是一次函数的应用,此类题是近年中考中的热点问题,关键是求出一次函数的解析式,应用一次函数的性质,解决实际问题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 464×104 | B. | 46.4×106 | C. | 4.64×106 | D. | 0.464×107 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
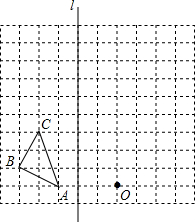 如图在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC、直线l和格点O.
如图在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC、直线l和格点O.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
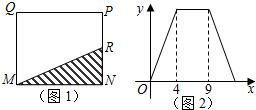 如图1,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.在这个变化过程中,变量x表示点R运动的路程,变量y表示△MNR的面积,图2表示变量y随x的变化情况,则当y=9时,点R所在的边是:PN边或QM边.
如图1,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.在这个变化过程中,变量x表示点R运动的路程,变量y表示△MNR的面积,图2表示变量y随x的变化情况,则当y=9时,点R所在的边是:PN边或QM边.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
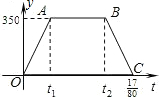 沪杭高速铁路已建成通车,某校研究性学习小组以此为课题,在研究列车的行驶速度时,得到一个数学问题.如图,若v是关于t的函数,图象为折线O-A-B-C,其中A(t1,350),B(t2,350),C($\frac{17}{80}$,0),四边形OABC的面积为70,则t2-t1=$\frac{3}{16}$.
沪杭高速铁路已建成通车,某校研究性学习小组以此为课题,在研究列车的行驶速度时,得到一个数学问题.如图,若v是关于t的函数,图象为折线O-A-B-C,其中A(t1,350),B(t2,350),C($\frac{17}{80}$,0),四边形OABC的面积为70,则t2-t1=$\frac{3}{16}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
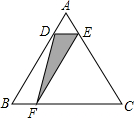 如图,在等边△ABC中,点D是AB边上的动点,过点作DE∥BC交边AC于点E,过点作EF∥AB交边BC于点F.连结DF,设动点D从点A出发沿AB匀速向点B运动,运动时间为t,则在整个运动过程中,△DEF的面积S与运动时间t的大致图象是( )
如图,在等边△ABC中,点D是AB边上的动点,过点作DE∥BC交边AC于点E,过点作EF∥AB交边BC于点F.连结DF,设动点D从点A出发沿AB匀速向点B运动,运动时间为t,则在整个运动过程中,△DEF的面积S与运动时间t的大致图象是( )| A. | 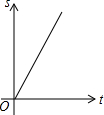 | B. | 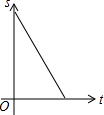 | C. | 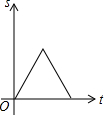 | D. | 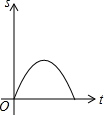 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com