
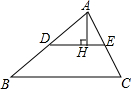
 如图,在△ABC中,点D、E分别是AB、AC的中点,AH⊥DE于点H,已知AH=3,BC=10,则S△ABC=30.
如图,在△ABC中,点D、E分别是AB、AC的中点,AH⊥DE于点H,已知AH=3,BC=10,则S△ABC=30. 分析 延长AH交BC于G,先证明DE是△ABC的中位线,由三角形中位线定理得出DE∥BC,DE=$\frac{1}{2}$BC,得出△ADE∽△ABC,由相似三角形的性质得出$\frac{AH}{AG}=\frac{DE}{BC}=\frac{1}{2}$,求出AG,即可得出结果.
解答 解:延长AH交BC于G,如图所示: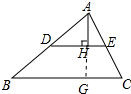
∵点D、E分别是AB、AC的中点,
∴DE是△ABC的中位线,
∴DE∥BC,DE=$\frac{1}{2}$BC,
∴△ADE∽△ABC,
∴$\frac{AH}{AG}=\frac{DE}{BC}=\frac{1}{2}$,
∴AG=2AH=6,
∴S△ABC=$\frac{1}{2}$BC•AG=$\frac{1}{2}$×10×6=30;
故答案为:30.
点评 本题考查了相似三角形的判定与性质、三角形中位线定理、三角形面积的计算;熟练掌握相似三角形的判定与性质,证明三角形中位线是解决问题的关键.


 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案科目:初中数学 来源: 题型:解答题
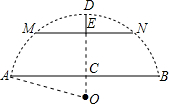 如图,有一石拱桥的桥拱是圆弧形,正常水位时水面宽AB=60m,水面到拱顶距离CD=18m.如果水面到拱顶的距离小于3.8m,需要采取紧急措施以防流水对桥的危害.现洪水经过,测得水面宽MN=32m,此时是否需要采取紧急措施?请说明理由.
如图,有一石拱桥的桥拱是圆弧形,正常水位时水面宽AB=60m,水面到拱顶距离CD=18m.如果水面到拱顶的距离小于3.8m,需要采取紧急措施以防流水对桥的危害.现洪水经过,测得水面宽MN=32m,此时是否需要采取紧急措施?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
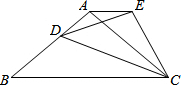 如图,在等腰三角形ABC中,AB=AC,D是AB边上一点,以CD为一边,向上作等腰△DCE,使△EDC∽△ABC,连AE,求证:
如图,在等腰三角形ABC中,AB=AC,D是AB边上一点,以CD为一边,向上作等腰△DCE,使△EDC∽△ABC,连AE,求证:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
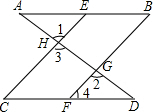 把下面的说理过程补充完整:
把下面的说理过程补充完整:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
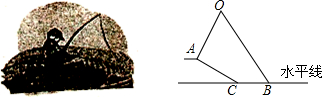
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2 | B. | 1 | C. | 2 | D. | -1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com