
【题目】如图,一抛物线经过点A(﹣2,0),点B(0,4)和点C(4,0),该抛物线的顶点为D.
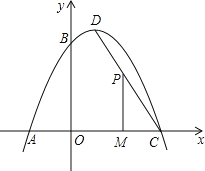
(1)求该抛物线的函数关系式及顶点D坐标.
(2)如图,若P为线段CD上的一个动点,过点P作PM⊥x轴于点M,求四边形PMAB的面积的最大值和此时点P的坐标.
(3)过抛物线顶点D,作DE⊥x轴于E点,F(m,0)是x轴上一动点,若以BF为直径的圆与线段DE有公共点,求m的取值范围.
【答案】(1)y=﹣![]() +x+4.D的坐标为(1,
+x+4.D的坐标为(1,![]() ).(2)点P的坐标为(
).(2)点P的坐标为(![]() ,1).(3)m的取值范围为﹣3≤m≤
,1).(3)m的取值范围为﹣3≤m≤![]() .
.
【解析】
试题分析:(1)设抛物线的解析式为y=a(x+2)(x﹣4),把(0,4)代入求得a=﹣![]() ,从而可求得抛物线的解析式,然后依据配方法可求得抛物线的顶点坐标;
,从而可求得抛物线的解析式,然后依据配方法可求得抛物线的顶点坐标;
(2)依据待定系数法可求得直线CD的解析式为y═﹣![]() x+6.设点P的坐标为(a,﹣
x+6.设点P的坐标为(a,﹣![]() a+6),则PM=﹣
a+6),则PM=﹣![]() a+6,然后根据SPMAB=S△AOB+SPMOB可求得四边形PMAB的面积与a的函数关系式,最后依据配方法可求得四边形的最大面积以及点P的坐标;
a+6,然后根据SPMAB=S△AOB+SPMOB可求得四边形PMAB的面积与a的函数关系式,最后依据配方法可求得四边形的最大面积以及点P的坐标;
(3)先依据勾股定理可求得BF2=m2+16,即r=![]() ,当如图1所示;当圆G与DE相切时,GH=r=(1﹣
,当如图1所示;当圆G与DE相切时,GH=r=(1﹣![]() )得到(1﹣
)得到(1﹣![]() )2=
)2=![]() +4,可求得m=﹣3,
+4,可求得m=﹣3,
如图2所示:点F在点E右侧且该圆经过点D时.由两点间的距离公式可知DG2=r2=(![]() )2+(
)2+(![]() )2可知
)2可知![]() +4=(
+4=(![]() ﹣1)2+(
﹣1)2+(![]() )2,从而可解得m=
)2,从而可解得m=![]() ,故此可求得m的取值范围是﹣3≤m≤
,故此可求得m的取值范围是﹣3≤m≤![]() .
.
解:(1)由题意设y=a(x+2)(x﹣4),把(0,4)代入得:﹣8a=4,
解得:a=﹣![]() .
.
∴该抛物线的解析式为y=﹣![]() (x+2)(x﹣4).
(x+2)(x﹣4).
整理得:y=﹣![]() +x+4.
+x+4.
∵y=﹣![]() +x+4=﹣
+x+4=﹣![]() (x﹣1)2+
(x﹣1)2+![]() ,
,
∴顶点D的坐标为(1,![]() ).
).
(2)设直线CD的函数关系式为y=kx+b,
∵把C(4,0),D(1,![]() )代入得k=﹣
)代入得k=﹣![]() ,b=6,
,b=6,
∴直线CD的函数关系式为y=﹣![]() x+6.
x+6.
设点P的坐标为(a,﹣![]() a+6),
a+6),
∵SPMAB=S△AOB+SPMOB,
∴四边形PMAB的面积=![]() ×2×4+
×2×4+![]() ×(﹣
×(﹣![]() a+6+4)×a=﹣
a+6+4)×a=﹣![]() a2+5a+4=﹣
a2+5a+4=﹣![]() (a﹣
(a﹣![]() )2+
)2+![]() .
.
∴当a=![]() 时,四边形PMAB的面积最大,最大面积为
时,四边形PMAB的面积最大,最大面积为![]() .
.
∴点P的坐标为(![]() ,1).
,1).
(3)∵点F的坐标为(m,0),点B的坐标为(0,4)
∴圆心G的坐标为(![]() ,2).
,2).
在Rt△BOF中由勾股定理可知:BF2=OB2+OF2=16+m2=4r2.
①如图1所示;当圆G与DE相切时.
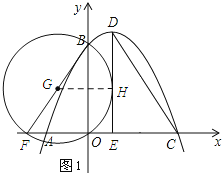
∵DE与圆G相切,
∴r=1﹣![]() .
.
r2=![]() +4.
+4.
∴(1﹣![]() )2=
)2=![]() +4.
+4.
解得:m=﹣3.
②如图2所示:点F在点E右侧且该圆经过点D时.
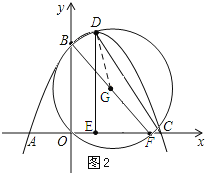
∵点D在圆G上,
∴DG2=(![]() )2+(
)2+(![]() )2=r2.
)2=r2.
∴![]() +4=(
+4=(![]() ﹣1)2+(
﹣1)2+(![]() )2.
)2.
解得:m=![]() .
.
综上所述,m的取值范围为﹣3≤m≤![]() .
.


科目:初中数学 来源: 题型:
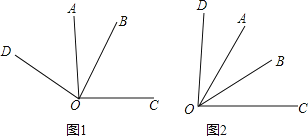
【题目】已知∠AOC=∠BOD=α(0°<α<180°)
(1)如图1,若α=90°
①写出图中一组相等的角(除直角外) ,理由是
②试猜想∠COD和∠AOB在数量上是相等、互余、还是互补的关系,并说明理由;
(2)如图2,∠COD+∠AOB和∠AOC满足的等量关系是 ;当α= °,∠COD和∠AOB互余.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解学生家长对孩子使用手机的态度情况,随机抽取部分学生家长进行问卷调查,发出问卷140份,每位学生家长1份,每份问卷仅表明一种态度,将回收的问卷进行整理(假设回收的问卷都有效),并绘制了如图两幅不完整的统计图.
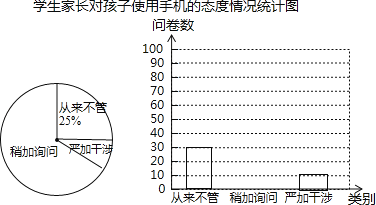
根据以上信息解答下列问题:
(1)回收的问卷数为 份,“严加干涉”部分对应扇形的圆心角度数为 .
(2)把条形统计图补充完整
(3)若将“稍加询问”和“从来不管”视为“管理不严”,已知全校共1500名学生,请估计该校对孩子使用手机“管理不严”的家长大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的有( )
(1)若ac=bc,则a=b;
(2)若![]() ,则a=﹣b;
,则a=﹣b;
(3)若x2=y2,则﹣4ax2=﹣4by2;
(4)若方程2x+5a=11﹣x与6x+3a=22的解相同,则a的值为0.
A.4 B.3 C.2 D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某饰品店以20元/件的价格采购了一批今年新上市的饰品进行了为期30天的销售,销售结束后,得知日销售量P(件)与销售时间x(天)之间有如下关系:P=﹣2x+80(1≤x≤30);又知前20天的销售价格Q1(元/件)与销售时间x(天)之间有如下关系:Q1=![]() x+30(1≤x≤20),后10天的销售价格Q2则稳定在45元/件.
x+30(1≤x≤20),后10天的销售价格Q2则稳定在45元/件.
(1)试分别写出该商店前20天的日销售利润R1(元)和后10天的日销售利润R2(元)与销售时间x(天)之间的函数关系式;
(2)请问在这30天的销售期中,哪一天的日销售利润最大?并求出这个最大利润值.
(注:销售利润=销售收入﹣购进成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】成都地铁自开通以来,发展速度不断加快,现已成为成都市民主要出行方式之一.今年4月29日成都地铁安全运输乘客约181万乘次,又一次刷新客流纪录,这也是今年以来第四次客流纪录的刷新,用科学记数法表示181万为( )
A.18.1×105 B.1.81×106 C.1.81×107 D.181×104
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com