
����Ŀ��ij��Ʒ����20Ԫ/���ļ۸�ɹ���һ�����������е���Ʒ������Ϊ��30������ۣ����۽�����֪��������P������������ʱ��x���죩֮�������¹�ϵ��P=��2x+80��1��x��30������֪ǰ20������ۼ۸�Q1��Ԫ/����������ʱ��x���죩֮�������¹�ϵ��Q1=![]() x+30��1��x��20������10������ۼ۸�Q2���ȶ���45Ԫ/����
x+30��1��x��20������10������ۼ۸�Q2���ȶ���45Ԫ/����
��1���Էֱ�д�����̵�ǰ20�������������R1��Ԫ���ͺ�10�������������R2��Ԫ��������ʱ��x���죩֮��ĺ�����ϵʽ��
��2����������30����������У���һ�����������������������������ֵ��
��ע����������=�������멁�����ɱ���
���𰸡���1��![]() ����2���ڵ�21��ʱ����������������������Ϊ950Ԫ��
����2���ڵ�21��ʱ����������������������Ϊ950Ԫ��
��������
�����������1������������Էֱ�ʾ�����̵�ǰ20�������������R1��Ԫ���ͺ�10�������������R2��Ԫ��������ʱ��x���죩֮��ĺ�����ϵʽ��
��2���е�һ���еĺ�����ϵʽ���Էֱ�����ڸ��Է�Χ�ڵ����ֵ��Ȼ����бȽϼ��ɽ���⣮
�⣺��1��������ɵã�
R1=P��Q1��20��=����2x+80��[��![]() x+30����20]=��x2+20x+800��
x+30����20]=��x2+20x+800��
R2=P��Q2��20��=����2x+80����45��20��=��50x+2000��
�����̵�ǰ20�������������R1��Ԫ���ͺ�10�������������R2��Ԫ��������ʱ��x���죩֮��ĺ�����ϵʽ�ֱ��ǣ�![]() ��
��
��2������1��x��20ʱ��R1=����x��10��2+900��
����x=10ʱ��R1�����ֵΪ900��
��21��x��30ʱ��R2=��50x+2000��
��R2��ֵ��xֵ���������С������x=21ʱ��R2�����ֵ��950��
��950��900��
���ڵ�21��ʱ����������������������Ϊ950Ԫ��


 ���Ž�������С״Ԫϵ�д�
���Ž�������С״Ԫϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾ȥ��1~3��ƽ��ÿ�¿���1.7��Ԫ��4~6��ƽ��ÿ��ӯ��1.8��Ԫ��7~10��ƽ��ÿ��ӯ��1.9��Ԫ��11��12��ƽ��ÿ�¿���2.5��Ԫ���������˾ȥ���ܵ�ӯ�������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס��ҡ������صĺ��θ߶ȷֱ�Ϊ20�ס���5�ס��ͣ�10�ף���ô��ߵĵط�����͵ĵط��� ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�����߾�����A����2��0������B��0��4���͵�C��4��0�����������ߵĶ���ΪD��
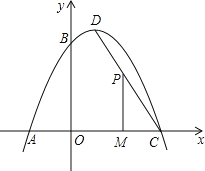
��1����������ߵĺ�����ϵʽ������D���꣮
��2����ͼ����PΪ�߶�CD�ϵ�һ�����㣬����P��PM��x���ڵ�M�����ı���PMAB����������ֵ�ʹ�ʱ��P�����꣮
��3���������߶���D����DE��x����E�㣬F��m��0����x����һ���㣬����BFΪֱ����Բ���߶�DE�й����㣬��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��l1��y=x+3��x�ύ�ڵ�A����y�ύ�ڵ�B����ֱ��l2��y=��![]() x���ڵ�P��ֱ��l3��y=��
x���ڵ�P��ֱ��l3��y=��![]() x+4��x�ύ�ڵ�C����y�ύ�ڵ�D����ֱ��l1���ڵ�Q����ֱ��l2���ڵ�R��
x+4��x�ύ�ڵ�C����y�ύ�ڵ�D����ֱ��l1���ڵ�Q����ֱ��l2���ڵ�R��
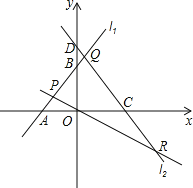
��1����A�������� ����B�������� ����P�������� ��
��2������POB��y���۵���P�Ķ�Ӧ��ΪP�䣬���жϵ�P���Ƿ���ֱ��l3�ϣ���˵�����ɣ�
��3������PQR�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ε����߳��ֱ���4��8����������������ε��ܳ�Ϊ�� ��
A��16 B��18 C��20 D��16��20
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC������AB��BC��CA���ֱ�Ϊ40��50��60����������ƽ���߽��ڵ�O����S��ABO��S��BCO��S��CAO= ��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com