
【题目】
![]()
(1)若1表示的点与﹣1表示的点重合,则﹣2表示的点与数 表示的点重合;
(2)若﹣1表示的点与3表示的点重合,5表示的点与数 表示的点重合;
(3)若数轴上A、B两点之间的距离为c个单位长度,点A表示的有理数是a,并且A、B两点经折叠后重合,请写出此时折线与数轴的交点表示的有理数是多少?
【答案】(1)2;(2)-3;(3)a+![]() c或a﹣
c或a﹣![]() c.
c.
【解析】试题分析:(1)根据对称的知识,若1表示的点与﹣1表示的点重合,则对称中心是原点,从而找到﹣2的对称点;
(2)若数﹣1表示的点与数3表示的点重合,则对称中心是1表示的点,从而找到5的对称点;根据对应点连线被对称中心平分,先找到对称中心,再找到点表示的数;从而求解;
(3)先得到A点与对称中心的距离,再进一步得到折线与数轴的交点表示的有理数.
解:(1)若1表示的点与﹣1表示的点重合,则﹣2表示的点与2表示的点重合;
(2)若﹣1表示的点与3表示的点重合,5表示的点与﹣3表示的点重合;
(3)若数轴上A、B两点之间的距离为c个单位长度,点A表示的有理数是a,并且A、B两点经折叠后重合,此时折线与数轴的交点表示的有理数是a+![]() c或a﹣
c或a﹣![]() c.
c.


科目:初中数学 来源: 题型:
【题目】某工程队修建一条总长为1860米的公路,在使用旧设备施工17天后,为尽快完成任务,工程队引进了新设备,从而将工作效率提高了50%,结果比原计划提前15天完成任务.
(1)工程队在使用新设备后每天能修路多少米?
(2)在使用旧设备和新设备工作效率不变的情况下,工程队计划使用旧设备m天,使用新设备n(16≤n≤26)天修建一条总长为1500米的公路,使用旧设备一天需花费16000元,使用新设备一天需花费25000元,当m、n分别为何值时,修建这条公路的总费用最少,并求出最少费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中有两点M(a,b),N(c,d),规定(a,b)⊕(c,d)=(a+c,b+d),则称点Q(a+c,b+d)为M,N的“和点”.若以坐标原点O与任意两点及它们的“和点”为顶点能构成四边形,则称这个四边形为“和点四边形”,现有点A(2,5),B(﹣1,3),若以O,A,B,C四点为顶点的四边形是“和点四边形”,则点C的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
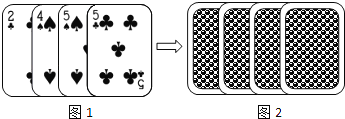
【题目】四张扑克牌的牌面如图1所示,将扑克牌洗匀后,如图2背面朝上放置在桌面上,小明和小亮设计了A、B两种游戏方案:
方案A:随机抽一张扑克牌,牌面数字为5时小明获胜;否则小亮获胜.
方案B:随机同时抽取两张扑克牌,两张牌面数字之和为偶数时,小明获胜;否则小亮获胜.
请你帮小亮选择其中一种方案,使他获胜的可能性较大,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列推理正确的是( )
A.∵a // d, b // c,∴c // d
B.∵ a // c,b // d,∴ c // d
C.∵ a // b,a // c,∴ b // c
D.∵ a // b,c // d,∴ a // c
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数的关系式是L1:y=kx2+(k﹣2)x﹣2
(1)下列说法中正确的序号有 :
①当k=1时,其顶点坐标为(![]() ,
,![]() );
);
②当k=2时,二次函数的图象关于y轴对称;
③无论k为何非零值,二次函数都经过(﹣1,0)和(0,﹣2);
(2)求证:无论k为何值时,函数图象与x轴总有交点;
(3)已知二次函数L1的图象与x轴相交于点A、B,顶点为P,若k>0,且△ABP为等边三角形,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在校田径运动会上,小明和其他三名选手参加100米预赛,赛场共设1,2,3,4四条跑道,选手以随机抽签的方式决定各自的跑道.若小明首先抽签,则小明抽到1号跑道的概率是( )
A. B. C. D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com