
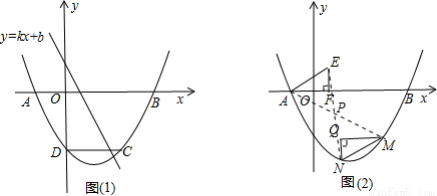
如图1,抛物线 经过A(-1,0),C(3,-2)两点,与
经过A(-1,0),C(3,-2)两点,与 轴交于点D,与
轴交于点D,与 轴交于另一点B.
轴交于另一点B.
(1)求此抛物线的解析式;
(2)若直线 (
( )将四边形ABCD面积二等分,求
)将四边形ABCD面积二等分,求 的值;
的值;
(3)如图2,过点E(1,1)作EF⊥ 轴于点F,将△AEF绕平面内某点P旋转180°得△MNQ(点M、N、Q分别与点A、E、F对应),使点M、N在抛物线上,求点N和点P的坐标?
轴于点F,将△AEF绕平面内某点P旋转180°得△MNQ(点M、N、Q分别与点A、E、F对应),使点M、N在抛物线上,求点N和点P的坐标?


(1) 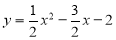 ;(2)
;(2) 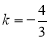 ;(3) (1,-3),(1,-1).
;(3) (1,-3),(1,-1).
【解析】
试题分析:把A、C两点坐标代入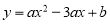 即可求出a、b的值,从而确定抛物线的解析式.
即可求出a、b的值,从而确定抛物线的解析式.
(1)∵抛物线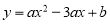 经过A(-1,0),C(3,-2),
经过A(-1,0),C(3,-2),
∴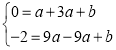 ,解之得:
,解之得: ,
,
∴所求抛物线的解析式为: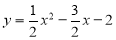 ;
;
(2)令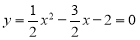 ,解得:x1=-1,x2=4,
,解得:x1=-1,x2=4,
∴B(4,0),
令x=0,可得:y=-2,
∴D(0,-2),
∵C(3,-2),
∴DC∥AB,
由勾股定理得:AD=BC=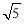 ,
,
∴四边形ADCB是等腰梯形,
∵D(0,-2),C(3,-2),∴取DC中点E,则E的坐标是( ,-2),
,-2),
过E作EF⊥AB于F,取EF的中点G,则G的坐标是( ,-1),
,-1),
则过G的直线(直线与AB和CD相交)都能把等腰梯形ABCD的面积二等份,
把G的坐标代入y=kx+1,得: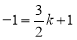 ,
,
∴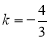 ;
;
(3)设Q(m,n),则M(m+2,n),N(m,n-1),
代入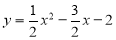 ,得:
,得: ,解之,得:
,解之,得: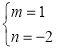 ,
,
∴Q(1,-2),M(3,-2),N(1,-3),
又Q的对应点为F(1,0),
∴QF的中点为旋转中心P,且P(1,-1),
∴点N、P的坐标分别为:(1,-3),(1,-1).
考点:二次函数综合题.


科目:初中数学 来源:2013-2014学年安徽省当涂县四校九年级上学期期末联考数学试卷(解析版) 题型:解答题
某菜农搭建了一个横截面为抛物线的大棚,尺寸如图:

(1)如图建立平面直角坐标系,使抛物线对称轴为y轴,求该抛物线的解析式;
(2)若需要开一个截面为矩形的门(如图所示),已知门的高度为1.60米,那么门的宽度最大是多少米(不考虑材料厚度)?(结果保留根号)
查看答案和解析>>
科目:初中数学 来源:2013-2014学年安徽十大名校九年级第四次月考数学试卷(解析版) 题型:选择题
长丰县是享誉全国的“草莓之乡”,2013年草莓种植面积达到了20万亩,品牌价值10.58亿元。10.58亿用科学记数法表示为
A.1.058×1010 B.1.058×109 C.10.58×109 D.10.58×108
查看答案和解析>>
科目:初中数学 来源:2013-2014学年四川省眉山市华兴联谊学校九年级下学期期中考试数学试卷(解析版) 题型:选择题
函数y=ax-a与y= (a≠0)在同一直角坐标系中的图像可能是( )
(a≠0)在同一直角坐标系中的图像可能是( )

查看答案和解析>>
科目:初中数学 来源:2013-2014学年四川省眉山市华兴联谊学校九年级下学期期中考试数学试卷(解析版) 题型:选择题
已知下列命题:
①若a >0,b>0,则a+b>0;
②若a2≠b2,则a ≠b
③角平分线上的点到角两边的距离相等;
④平行四边形的对角线互相平分
⑤直角三角形斜边上的中线等于斜边的一半。
其中原命题与逆命题均为真命题的是( )
A、①③④ B、①②④ C、③④⑤ D、②③⑤
查看答案和解析>>
科目:初中数学 来源:2013-2014学年四川省乐山市夹江县九年级毕业会考适应性考试数学试卷(解析版) 题型:解答题
如图,在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.直线BF垂直于直线CE于点F,交CD于点G.求证:AE=CG.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年四川省乐山市夹江县九年级毕业会考适应性考试数学试卷(解析版) 题型:填空题
小明和爸爸今年五一节准备到峨眉山去游玩,他们选择了报国寺、伏虎寺、清音阁三个景点去游玩.如果他们各自在这三个景点中任选一个景点作为游玩的第一站(每个景点被选为第一站的可能性相同),那么他们都选择报国寺为第一站的概率是 .
查看答案和解析>>
科目:初中数学 来源:2013-2014学年吉林省长春市朝阳区中考一模数学试卷(解析版) 题型:解答题
如图,在四边形ABCD中,∠ABC=30°,∠ADC=60°,AD=DC,连接AC、BD.在四边形ABCD的外部以BC为一边作等边三角形BCE,连接AE.
(1)求证:BD=AE;
(2)若AB=2,BC=3,求BD的长.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市顺义区中考二模数学试卷(解析版) 题型:选择题
如图,BD平分 ,CD⊥BD,D为垂足,
,CD⊥BD,D为垂足,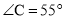 ,则
,则 的度数是( )
的度数是( )

A.35° B.55° C.60° D.70°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com