
如图,在Rt△ABC中,∠B=90°,AC=60,AB=30。点D是AC上的动点,过D作DF⊥BC于F,再过F作FE//AC,交AB于E。设CD=x,DF=y.
(1)求y与x的函数关系式;
(2)当四边形AEFD为菱形时,求x的值;
(3)当△FED是直角三角形时,求x的值.

(1) ;(2)40;(3)30.
;(2)40;(3)30.
【解析】
试题分析:(1)由已知,根据锐角三角函数定义和特殊角的三角函数值可得∠C=30°,从而在Rt△CDF中,再应用锐角三角函数定义和特殊角的三角函数值可得y与x的函数关系式.
(2)根据菱形四边相等的性质,由AD=DF即AC-CD=DF列方程求解.
(3)首先判断△FED是直角三角形只有∠FDE=90°,得出 ,解之即为所求.
,解之即为所求.
试题解析:(1)∵∠B=90°,AC=60,AB=30,
∴ .∴∠C=30°.∴
.∴∠C=30°.∴ .
.
∴y与x的函数关系式为 .
.
(2)当四边形AEFD为菱形时,有AD=DF,
∴AC-CD=DF,即 ,解得x=40.
,解得x=40.
∴当四边形AEFD为菱形时,x=40.
(3)如图,当△FED直角三角形是时,只能是∠FDE=90°,
∵DF⊥BC,∠B=90°,∴DF//AB.
又∵FE//AC,∴四边形AEFD为平行四边形. ∴AE=DF.
由DF⊥BC得∠2=90°,∴∠1=∠2. ∴DE//BC.
∴∠3=∠B=90°,∠4=∠C=30°.
在Rt△BOC中, ,即60-x= x,
,即60-x= x,
∴x=30.
∴当△FED是直角三角形时,x=30.
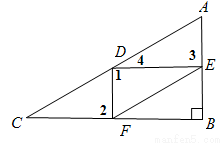
考点:1.单动点问题;2. 锐角三角函数定义;3.特殊角的三角函数值;4. 菱形四边的性质;5.方程思想的应用.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2014年初中毕业升学考试(广西南宁卷)数学(解析版) 题型:填空题
如图7,△ABC是等腰直角三角形,AC=BC= ,以斜边AB上的点O为圆心的圆分别与AC,BC相切与点E,F, 与AB 分别交于点G,H,且 EH 的延长线和 CB 的延长线交于点D,则 CD 的长为 .
,以斜边AB上的点O为圆心的圆分别与AC,BC相切与点E,F, 与AB 分别交于点G,H,且 EH 的延长线和 CB 的延长线交于点D,则 CD 的长为 .

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西北海卷)数学(解析版) 题型:选择题
甲、乙、丙、丁四人参加射击训练,每人各射击20次,他们射击成绩的平均数都是9.1环,各自的方差见如下表格:
| 甲 | 乙 | 丙 | 丁 |
方差 | 0.293 | 0.375 | 0.362 | 0.398 |
由上可知射击成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广东汕尾卷)数学(解析版) 题型:选择题
在我国南海某海域探明可燃冰储量约有194亿立方米.数字19 400 000 000用科学记数法表示正确的是( )
A. B.
B. C.
C. D.
D. 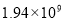
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广东梅州卷)数学(解析版) 题型:解答题
某县为了解七年级学生对篮球、羽毛球、乒乓球、足球(以下分别用A、B、C、D表示)这四种球类运动的喜爱情况(每人只能选一种),对全县七年级学生进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).

请根据以上信息回答:
(1)本次参加抽样调查的学生有 人;
(2)若全县七年级学生有4000人,估计喜爱足球(D)运动的人数是 人;
(3)在全县七年级学生中随机抽查一位,那么该学生喜爱乒乓球(C)运动的概率是 .
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(安徽卷)数学(解析版) 题型:解答题
若两个二次函数图象的顶点,开口方向都相同,则称这两个二次函数为“同簇二次函数”。
(1)请写出两个为“同簇二次函数”的函数;
(2)已知关于x的二次函数y1=2x2—4mx+2m2+1,和y2=ax2+bx+5,其中y1的图象经过点A(1,1),若y1+y2为y1为“同簇二次函数”,求函数y2的表达式,并求当0≤x≤3时,y2的最大值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com