Question

若两个二次函数图象的顶点，开口方向都相同，则称这两个二次函数为“同簇二次函数”。

（1）请写出两个为“同簇二次函数”的函数；

（2）已知关于x的二次函数y1=2x2—4mx+2m2+1，和y2=ax2+bx+5，其中y1的图象经过点A（1，1），若y1+y2为y1为“同簇二次函数”，求函数y2的表达式，并求当0≤x≤3时，y2的最大值。

 

Answer 1

（1）本题为开放题，答案不唯一，符合题意即可，如：；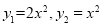

（2），当时，的最大值为20.

【解析】

试题分析：（1）本题为开放题，答案不唯一，符合题意即可，如：；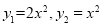

（2）把点A（1,1）代入函数的解析式，可解得，于是得到；因为与是“同簇二次函数”，可设，于是得到.将点（0,5）代入上式，可求得k的值，从而求得函数y2的表达式.再根据的函数图象即可求得当时， 的最大值.

试题解析：（1）本题为开放题，答案不唯一，符合题意即可，如：；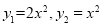

（2）∵函数的图象经过点A（1,1），则，解得，

∴.

解法一：∵与是“同簇二次函数”，∴可设，

则。

由题意可知函数的图象经过点（0,5），则，∴k-2=5，∴.

解法二：∵与是“同簇二次函数”，

∴，

∴，化简得b=-2a，

又，将代入，解得a=5，b=-10，

∴.

当时，根据的函数图象可知，的最大值=.

考点：二次函数综合题.