
【题目】新型冠状病毒感染的肺炎疫情牵动着全国人民的心,来自全国四面八方的救援物资快速向疫区汇聚.我省某食品公司向武汉捐献一批饮用水和蔬菜共320件,一件饮用水与一件蔬菜价格的比是2:5,饮用水总价4万元,蔬菜总价6万元.请解答下列问题:
(1)求饮用水和蔬菜各有多少件?
(2)现计划租用甲、乙两种型号的货车共8辆,一次性将这批饮用水和蔬菜全部运往受灾地区某中学.已知每辆甲型货车最多可装饮用水40件和蔬菜10件,每辆乙型货车最多可装饮用水和蔬菜各20件,则该单位安排甲、乙两种货车时有几种方案?请你帮助设计出来;
(3)在(2)的条件下,如果甲型货车每辆需付运费400元,乙型货车每辆需付运费360元,该单位应选择哪种方案可使运费最少?最少运费是多少?
【答案】(1)饮用水和蔬菜分别为200件和120件;(2)安排甲.乙两种型号的货车时有3种方案:方案①:甲车2辆,乙车6辆;方案②:甲车3辆,乙车5辆;方案③:甲车4辆,乙车4辆;(3)运输部门应选择甲车2辆,乙车6辆,可使运费最少,最少运费是2960元.
【解析】
(1) 设饮用水有x件,则蔬菜有(320-x)件.根据一件饮用水与一件蔬菜价格的比是2:5列出方程;(2) 设租用甲型货车n辆.则租用乙型货车(8 -n)辆.根据关系式为:40×甲货车辆数+20×乙货车辆数≥200;10×甲货车辆数+20×乙货车辆数≥120,列方程;(3)分别计算出相应方案,比较即可.
(1) 设饮用水有x件.依题意.得
![]() :
:![]() =2:5.
=2:5.
解得x=200.
经检验x=200是原分式方程的解.且符合题意
..320 - 200= 120(件).
答:饮用水和蔬菜分别为200件和120件.
(2)设租用甲型货车n辆.则租用乙型货车(8 -n)辆.
依题意,得![]() .
.
解这个不等式组,得2≤n≤4.∵n为整数,
∴n=2或3或4.
安排甲.乙两种型号的货车时有3种方案:
∴方案①:甲车2辆,乙车6辆;
方案②:甲车3辆,乙车5辆;
方案③:甲车4辆,乙车4辆.
(3) 3种方案的运费分别为:
方案①:2×400+6×360=2960(元);
方案②:3×400+5×360=3000(元);
方案③:4×400+4×360=3040(元).
方案①运费最少,最少运费是2960元.
答;运输部门应选择甲车2辆,乙车6辆,可使运费最少,最少运费是2960元


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】现有5张除正面数字外完全相同的卡片,正面数字分别为1,2,3,4,5,将卡片背面朝上洗匀,从中随机抽出一张记下数字后放回,洗匀后再次随机抽出一张,则抽出的两张卡片上所写数字相同的概率______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级共有四个班,各班人数比例如图1所示.在一次数学考试中,四个班的平均成绩如图2所示.

(1)四个班平均成绩的中位数是________;
(2)下列说法:①3班85分以上人数最少;②1,3两班的平均分差距最小;③本次考试年段成绩最高的学生在4班.其中正确的是________(填序号);
(3)若用公式![]() (m,n分别表示各班平均成绩)分别计算1,2两班和3,4两班的平均成绩,哪两班的计算结果会与实际平均成绩相同,请说明理由.
(m,n分别表示各班平均成绩)分别计算1,2两班和3,4两班的平均成绩,哪两班的计算结果会与实际平均成绩相同,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】金松科技生态农业养殖有限公司种植和销售一种绿色羊肚菌,已知该羊肚菌的成本是12元/千克,规定销售价格不低于成本,又不高于成本的两倍.经过市场调查发现,某天该羊肚菌的销售量y(千克)与销售价格x(元/千克)的函数关系如下图所示:

(1)求y与x之间的函数解析式;
(2)求这一天销售羊肚菌获得的利润W的最大值;
(3)若该公司按每销售一千克提取1元用于捐资助学,且保证每天的销售利润不低于3600元,问该羊肚菌销售价格该如何确定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在一条笔直的道路上相向而行,甲骑自行车从A地到B地,乙驾车从B地到A地,他们分别以不同的速度匀速行驶,已知甲先出发6分钟后,乙才出发,在整个过程中,甲、乙两人的距离y(千米)与甲出发的时间x(分)之间的关系如图所示,当乙到达终点A时,甲还需 分钟到达终点B.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高校为了解本校学生出行使用共享单车的情况,随机调查了某天部分出行学生使用共享单车的情况,并整理成如下统计表.
使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
人数 | 11 | 15 | 23 | 28 | 18 | 5 |
(1)这天部分出行学生使用共享单车次数的中位数是 ,众数是 .
(2)这天部分出行学生平均每人使用共享单车约多少次?(结果保留整数)
(3)若该校某天有1500名学生出行,请你估计这天使用共享单车次数在3次以上(含3次)的学生有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,AE=CG,AH=CF.
(1)求证:△AEH≌△CGF;
(2)若EG平分∠HEF,求证:四边形EFGH是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
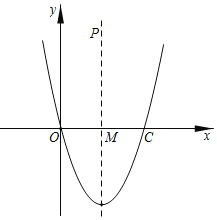
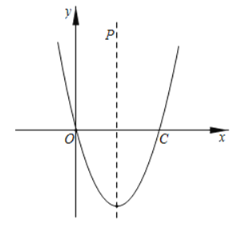
【题目】已知抛物线顶点坐标为![]() ,且与
,且与![]() 轴交于原点和点
轴交于原点和点![]() .对称轴与
.对称轴与![]() 轴交点为
轴交点为![]() .
.
(1)求抛物线的解析式;
(2)若点![]() 在抛物线上,且横坐标为
在抛物线上,且横坐标为![]() ,在抛物线对称轴上找一点
,在抛物线对称轴上找一点![]() ,使得
,使得![]() 与
与![]() 的差最大,求此时点
的差最大,求此时点![]() 的坐标;
的坐标;
(3)若点![]() 在抛物线的对称轴上,且纵坐标为
在抛物线的对称轴上,且纵坐标为![]() .探究:在抛物线上是否存在点
.探究:在抛物线上是否存在点![]() 使得
使得![]() 四点共圆?若存在求出点
四点共圆?若存在求出点![]() 坐标;若不存在请说明理由.
坐标;若不存在请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com