
【题目】已知抛物线顶点坐标为![]() ,且与
,且与![]() 轴交于原点和点
轴交于原点和点![]() .对称轴与
.对称轴与![]() 轴交点为
轴交点为![]() .
.
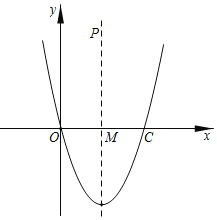
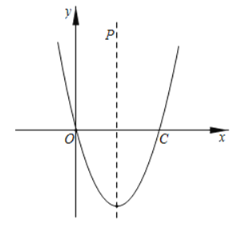
(1)求抛物线的解析式;
(2)若点![]() 在抛物线上,且横坐标为
在抛物线上,且横坐标为![]() ,在抛物线对称轴上找一点
,在抛物线对称轴上找一点![]() ,使得
,使得![]() 与
与![]() 的差最大,求此时点
的差最大,求此时点![]() 的坐标;
的坐标;
(3)若点![]() 在抛物线的对称轴上,且纵坐标为
在抛物线的对称轴上,且纵坐标为![]() .探究:在抛物线上是否存在点
.探究:在抛物线上是否存在点![]() 使得
使得![]() 四点共圆?若存在求出点
四点共圆?若存在求出点![]() 坐标;若不存在请说明理由.
坐标;若不存在请说明理由.
【答案】(1)![]() 即
即![]() ;(2)
;(2)![]() ;(3)Q(5,5)或(
;(3)Q(5,5)或(![]() )或(
)或(![]() ).
).
【解析】
(1)设抛物线的解析式为y=a(x-2)2-4,解方程即可得到结论;
(2)由(1)知,抛物线的解析式为y=x2-4x,解方程得到C(4,0),求得A(-2,12),而抛物线的对称轴为x=2,根据三角形三边关系定理之两边之差小于第三边,即可得到结论;
(3)由(2)知,抛物线的对称轴为直线x=2,求得P(2,8),由点O、M、P、Q四点共圆,得到点Q是Rt△OMP外接圆上,设Q坐标为(m,n),则m2-4m=n①,解方程即可得到结论.
解:(1)∵抛物线顶点坐标为(2,-4),
∴设抛物线的解析式为y=a(x-2)2-4,
∵抛物线过原点,
∴0=a(0-2)2-4,
∴a=1,
∴抛物线的解析式为y=(x-2)2-4=x2-4x;
(2)由(1)知,抛物线的解析式为y=x2-4x,
令y=0,则x2-4x=0,
∴x=0或x=4,
∴C(4,0),
∵A点的横坐标为-2,
∴y=4-4×(-2)=12,
∴A(-2,12),
而抛物线的对称轴为x=2,
∴点C(4,0)关于抛物线的对称轴x=2的对称点为O(0,0),
则过点O,A的直线与抛物线的对称轴的交点为点B,理由是三角形三边关系定理之两边之差小于第三边,
∵A(-2,12),
∴直线OA的解析式为y=-6x,
当x=2时,y=-12,
∴点B(2,-12);
(3)由(2)知,抛物线的对称轴为直线x=2,
∴P(2,8),
∵抛物线的对称轴与x轴交点为M,
∴M(2,0),
∴∠OMP=90°,
∵点O、M、P、Q四点共圆,则点Q是Rt△OMP外接圆上,
∴点Q到OP的中点的距离等于半径![]() OP=
OP=![]() ×
×![]() ,而OP的中点坐标为(1,4),
,而OP的中点坐标为(1,4),
由(1)知,抛物线的解析式为y=x2-4x,设Q坐标为(m,n),则m2-4m=n①,
∴(m-1)2+(n-4)2=17②,∴m2-2m+n2-8n=0,
而m2-2m+(m2-4m)2-8(m2-4m)=m2-2m+m2(m-4)2-8m(m-4)
=m[m-2+m(m-4)2-8(m-4)]=m[(m-5)+(m-5)(m-4)2+5(m-4)2-8(m-5)+3-8]
=m{(m-5)+(m-5)(m-4)2+5[(m-5)2+2(m-5)+1]-8(m-5)-5}
=m[(m-5)+(m-5)(m-4)2+5(m-5)2+10(m-5)-8(m-5)]
=m(m-5)[1+(m-4)2+5(m-5)+2]
=m(m-5)(m2-3m-6)
∴m(m-5)(m2-3m-6)=0,
∴m=0(舍)或m=5或m2-3m-6=0,
∴m=5或m=![]() ,
,
∴Q(5,5)或(![]() )或(
)或(![]() ).
).


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:初中数学 来源: 题型:
【题目】新型冠状病毒感染的肺炎疫情牵动着全国人民的心,来自全国四面八方的救援物资快速向疫区汇聚.我省某食品公司向武汉捐献一批饮用水和蔬菜共320件,一件饮用水与一件蔬菜价格的比是2:5,饮用水总价4万元,蔬菜总价6万元.请解答下列问题:
(1)求饮用水和蔬菜各有多少件?
(2)现计划租用甲、乙两种型号的货车共8辆,一次性将这批饮用水和蔬菜全部运往受灾地区某中学.已知每辆甲型货车最多可装饮用水40件和蔬菜10件,每辆乙型货车最多可装饮用水和蔬菜各20件,则该单位安排甲、乙两种货车时有几种方案?请你帮助设计出来;
(3)在(2)的条件下,如果甲型货车每辆需付运费400元,乙型货车每辆需付运费360元,该单位应选择哪种方案可使运费最少?最少运费是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
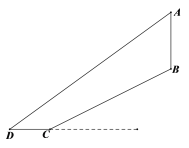
【题目】某游乐场新推出一个“极速飞车”的项目.项目有两条斜坡轨道以满足不同的难度需求,游客可以乘坐垂直升降电梯AB自由上下选择项目难度,其中斜坡轨道BC的坡度为![]() ,BC=
,BC=![]() 米,CD=8米,∠D=36°,(其中A,B,C,D均在同一平面内)则垂直升降电梯AB的高度约为__________米.(精确到0.1米,参考数据:
米,CD=8米,∠D=36°,(其中A,B,C,D均在同一平面内)则垂直升降电梯AB的高度约为__________米.(精确到0.1米,参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系![]() 中,点
中,点![]() 的坐标为
的坐标为![]() ,
,![]() 是第一象限内任意一点,连接
是第一象限内任意一点,连接![]() 、
、![]() ,若
,若![]() ,
,![]() ,则
,则![]() 就叫做点
就叫做点![]() 的“双角坐标”.例如:点
的“双角坐标”.例如:点![]() 的“双角坐标”为
的“双角坐标”为![]() .若点
.若点![]() 到
到![]() 轴的距离为
轴的距离为![]() ,则
,则![]() 的最小值为___.
的最小值为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
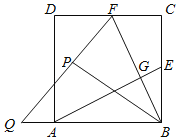
【题目】如图,正方形ABCD中,E、F分别为BC、CD的中点,连接AE,BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交BA延长线于点Q,下列结论①AE=BF;②AE⊥BF;③S四边形ECFG=2S△BGE.正确的有_____.(填正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
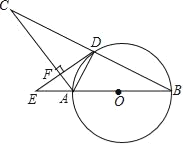
【题目】如图,在等腰△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D且BD=2AD,过点D作DE⊥AC交BA延长线于点E,垂足为点F.
(1)求tan∠ADF的值;
(2)证明:DE是⊙O的切线;
(3)若⊙O的半径R=5,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
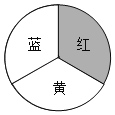
【题目】某商场开业,为了活跃气氛,用红、黄、蓝三色均分的转盘设计了两种抽奖方案,凡来商场消费的顾客都可以选择一种抽奖方案进行抽奖(若指针恰好停在分割线上则重转).
方案一:转动转盘一次,指针落在红色区域可领取一份奖品;
方案二:转动转盘两次,指针落在不同颜色区域可领取一份奖品.
(1)若选择方案一,则可领取一份奖品的概率是 ;
(2)选择哪个方案可以使领取一份奖品的可能性更大?请用列表法或画树状图法说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com