
【题目】已知在平面直角坐标系![]() 中,点
中,点![]() 的坐标为
的坐标为![]() ,
,![]() 是第一象限内任意一点,连接
是第一象限内任意一点,连接![]() 、
、![]() ,若
,若![]() ,
,![]() ,则
,则![]() 就叫做点
就叫做点![]() 的“双角坐标”.例如:点
的“双角坐标”.例如:点![]() 的“双角坐标”为
的“双角坐标”为![]() .若点
.若点![]() 到
到![]() 轴的距离为
轴的距离为![]() ,则
,则![]() 的最小值为___.
的最小值为___.
科目:初中数学 来源: 题型:
【题目】甲、乙两人在一条笔直的道路上相向而行,甲骑自行车从A地到B地,乙驾车从B地到A地,他们分别以不同的速度匀速行驶,已知甲先出发6分钟后,乙才出发,在整个过程中,甲、乙两人的距离y(千米)与甲出发的时间x(分)之间的关系如图所示,当乙到达终点A时,甲还需 分钟到达终点B.

查看答案和解析>>
科目:初中数学 来源: 题型:
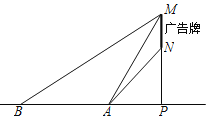
【题目】某数学社团成员想利用所学的知识测量某广告牌的宽度![]() 图中线段MN的长
图中线段MN的长![]() ,直线MN垂直于地面,垂足为点
,直线MN垂直于地面,垂足为点![]() 在地面A处测得点M的仰角为
在地面A处测得点M的仰角为![]() 、点N的仰角为
、点N的仰角为![]() ,在B处测得点M的仰角为
,在B处测得点M的仰角为![]() ,
,![]() 米,且A、B、P三点在一直线上
米,且A、B、P三点在一直线上![]() 请根据以上数据求广告牌的宽MN的长.
请根据以上数据求广告牌的宽MN的长.
![]() 参考数据:
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC 中,AB=AC=6cm,∠B=∠C,BC=4cm,点 D 为 AB的中点.
(1)如果点 P 在线段 BC 上以 1cm/s 的速度由点 B 向点 C 运动,同时,点 Q 在线段 CA 上由点 C 向点 A 运动.
①若点 Q 的运动速度与点 P 的运动速度相等,经过 1 秒后,△BPD 与△CQP 是否全等,请说明理由;
②若点 Q 的运动速度与点 P 的运动速度不相等,当点 Q 的运动速度为多少时,能够使△BPD 与△CQP 全等?
(2)若点 Q 以②中的运动速度从点 C 出发,点 P 以原来的运动速度从点 B 同时出发,都逆时针沿△ABC 三边运动,则经过 后,点 P 与点 Q 第一次在△ABC 的 边上相遇?(在横线上直接写出答案,不必书写解题过程)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形的周长为60.
(1)当该矩形的面积为200时,求它的边长;
(2)请表示出这个矩形的面积与其一边长的关系,并求出当矩形面积取得最大值时,矩形的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线顶点坐标为![]() ,且与
,且与![]() 轴交于原点和点
轴交于原点和点![]() .对称轴与
.对称轴与![]() 轴交点为
轴交点为![]() .
.
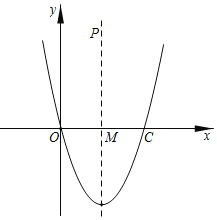
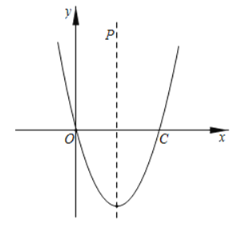
(1)求抛物线的解析式;
(2)若点![]() 在抛物线上,且横坐标为
在抛物线上,且横坐标为![]() ,在抛物线对称轴上找一点
,在抛物线对称轴上找一点![]() ,使得
,使得![]() 与
与![]() 的差最大,求此时点
的差最大,求此时点![]() 的坐标;
的坐标;
(3)若点![]() 在抛物线的对称轴上,且纵坐标为
在抛物线的对称轴上,且纵坐标为![]() .探究:在抛物线上是否存在点
.探究:在抛物线上是否存在点![]() 使得
使得![]() 四点共圆?若存在求出点
四点共圆?若存在求出点![]() 坐标;若不存在请说明理由.
坐标;若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了做好新冠肺炎疫情期间开学工作,我区某中学用药熏消毒法对教室进行消毒.已知一瓶药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例;药物释放完毕后,y与x成反比例,如图所示.根据图中提供的信息,解答下列问题:
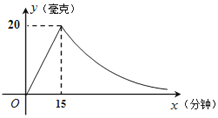
(1)写出倾倒一瓶药物后,从药物释放开始,y与x之间的两个函数关系式及相应的自变量取值范围;
(2)据测定,当空气中每立方米的含药量不低于8毫克时,消毒有效,那么倾倒一瓶药物后,从药物释放开始,有效消毒时间是多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(11·湖州)(本小题10分)
如图,已知E、F分别是□ABCD的边BC、AD上的点,且BE=DF。
⑴求证:四边形AECF是平行四边形;
⑵若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
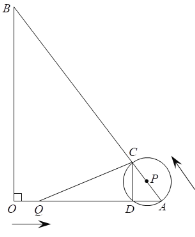
【题目】如图,在△AOB中,∠AOB=90°,OA=6,OB=8,动点Q从点O出发,沿着OA方向以1个单位长度/秒的速度匀速运动,同时动点P从点A出发,沿着AB方向也以1个单位长度/秒的速度匀速运动,设运动时间为t秒(0<t≤5),以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连结CD、CQ.
⑴ 当点Q与点D重合时,求t的值;
⑵ 若△ACQ是等腰三角形,求t的值;
⑶ 若⊙P与线段QC只有一个公共点,求t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com