
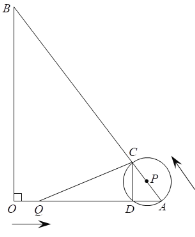
【题目】如图,在△AOB中,∠AOB=90°,OA=6,OB=8,动点Q从点O出发,沿着OA方向以1个单位长度/秒的速度匀速运动,同时动点P从点A出发,沿着AB方向也以1个单位长度/秒的速度匀速运动,设运动时间为t秒(0<t≤5),以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连结CD、CQ.
⑴ 当点Q与点D重合时,求t的值;
⑵ 若△ACQ是等腰三角形,求t的值;
⑶ 若⊙P与线段QC只有一个公共点,求t的取值范围.
【答案】(1) ![]() ;(2)
;(2) ![]() 或者
或者![]() 或者
或者![]() .;(3)
.;(3) ![]() 或者
或者![]()
【解析】
(1)点Q与点D重合时,先证明![]() ,得到
,得到![]() ,利用平行线分线段成比例,找出AD的长,利用OQ+DA=OA,求出t的值.
,利用平行线分线段成比例,找出AD的长,利用OQ+DA=OA,求出t的值.
(2)分三种情况进行讨论,AQ=AC;QC=CA;QC=QA,利用等腰三角形性质和三角形相似求出.
(3)一个交点,分情况讨论,当圆P与QC相切的时候,以及点Q与D重合的时候进行讨论,便可找出t的取值范围.
解:![]() CA是直径,∠AOB=90°.
CA是直径,∠AOB=90°.
![]()
![]() .
.
在△AOB中,∠AOB=90°,OA=6,OB=8中.
![]() .
.
![]()
![]() 即
即![]() .
.
![]()
![]()
![]()
![]()
当![]() 秒时,点Q与点D重合.
秒时,点Q与点D重合.
(2)若△ACQ是等腰三角形时,分三种情况讨论.
![]() ①当AQ=AC时,即AC=AQ=2t,OQ=t.
①当AQ=AC时,即AC=AQ=2t,OQ=t.
![]()
![]() 即:
即:![]() .
.
②当QC=CA时,即QC=CA=2t,由(1)知![]() .
.
![]()
![]()
![]() 即:
即:![]() .
.
③当QC=QA时,过点Q作![]() ,则AE=t,AQ=6-t
,则AE=t,AQ=6-t
![]() ∽
∽![]() .
.
![]() .
.
![]() 即:
即:![]() .
.
综上所述,当△ACQ是等腰三角形时,![]() 或者
或者![]() 或者
或者![]() .
.
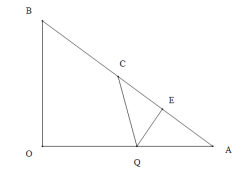
(3)当QC与圆P相切时,![]() .
.
![]()
![]() .
.
![]() .
.
![]() ∽
∽![]()
![]() 即:
即:![]() .
.
解得:![]()
当![]() 时,圆P与QC只有一个交点.
时,圆P与QC只有一个交点.
当![]() 时,由(1)知:
时,由(1)知:![]() .
.
当![]() 时,圆P与QC只有一个交点.
时,圆P与QC只有一个交点.
故:当圆P与QC只有 一个交点时,t的范围:![]() 或者
或者![]() .
.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系![]() 中,点
中,点![]() 的坐标为
的坐标为![]() ,
,![]() 是第一象限内任意一点,连接
是第一象限内任意一点,连接![]() 、
、![]() ,若
,若![]() ,
,![]() ,则
,则![]() 就叫做点
就叫做点![]() 的“双角坐标”.例如:点
的“双角坐标”.例如:点![]() 的“双角坐标”为
的“双角坐标”为![]() .若点
.若点![]() 到
到![]() 轴的距离为
轴的距离为![]() ,则
,则![]() 的最小值为___.
的最小值为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
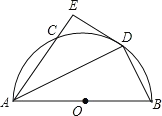
【题目】如图,![]() 是半圆
是半圆![]() 的直径,点
的直径,点![]() 是半圆上的一个动点,
是半圆上的一个动点,![]() 的角平分线交圆弧于点
的角平分线交圆弧于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() .
.
(1)求证:![]() 是半圆
是半圆![]() 的切线;
的切线;
(2)填空:①若![]() ,则
,则![]() __________;
__________;
②连接![]() 、
、![]() ,当
,当![]() 的度数为__________时,四边形
的度数为__________时,四边形![]() 是菱形.
是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着![]() 技术的发展,人们对各类
技术的发展,人们对各类![]() 产品的使用充满期待.某公司计划在某地区销售第一款
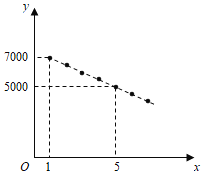
产品的使用充满期待.某公司计划在某地区销售第一款![]() 产品,根据市场分析,该产品的销售价格将随销售周期的变化而变化.设该产品在第
产品,根据市场分析,该产品的销售价格将随销售周期的变化而变化.设该产品在第![]() (
(![]() 为正整数)个销售周期每台的销售价格为
为正整数)个销售周期每台的销售价格为![]() 元,
元,![]() 与
与![]() 之间满足如图所示的一次函数关系.
之间满足如图所示的一次函数关系.
(1)求![]() 与
与![]() 之间的关系式;
之间的关系式;
(2)设该产品在第![]() 个销售周期的销售数量为
个销售周期的销售数量为![]() (万台),
(万台),![]() 与
与![]() 的关系可用
的关系可用![]() 来描述.根据以上信息,试问:哪个销售周期的销售收入最大?此时该产品每台的销售价格是多少元?
来描述.根据以上信息,试问:哪个销售周期的销售收入最大?此时该产品每台的销售价格是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生的安全意识情况,在全校范围内随机抽取部分学生进行问卷调查,根据调查结果,把学生的安全意识分成“淡薄”、“一般”、“较强”、“很强”四个层次,并绘制成如下两幅尚不完整的统计图.

根据以上信息,解答下列问题:
(1)这次调查一共抽取了 名学生,其中安全意识为“很强”的学生占被调查学生总数的百分比是 ;
(2)请将条形统计图补充完整;
(3)该校有1800名学生,现要对安全意识为“淡薄”、“一般”的学生强化安全教育,根据调查结果,估计全校需要强化安全教育的学生约有 名.
查看答案和解析>>
科目:初中数学 来源: 题型:
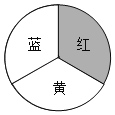
【题目】某商场开业,为了活跃气氛,用红、黄、蓝三色均分的转盘设计了两种抽奖方案,凡来商场消费的顾客都可以选择一种抽奖方案进行抽奖(若指针恰好停在分割线上则重转).
方案一:转动转盘一次,指针落在红色区域可领取一份奖品;
方案二:转动转盘两次,指针落在不同颜色区域可领取一份奖品.
(1)若选择方案一,则可领取一份奖品的概率是 ;
(2)选择哪个方案可以使领取一份奖品的可能性更大?请用列表法或画树状图法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=ax2+bx+![]() 与x轴分别交于点A(﹣1,0),B(3,0),点C是顶点.
与x轴分别交于点A(﹣1,0),B(3,0),点C是顶点.
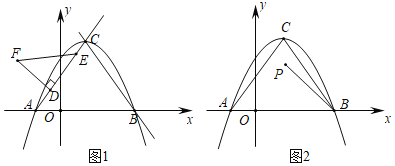
(1)求抛物线的解析式;
(2)如图1,线段DE是射线AC上的一条动线段(点D在点E的下方),且DE=2,点D从点A出发沿着射线AC的方向以每秒2个单位长度的速度运动,以DE为一边在AC上方作等腰Rt△DEF,其中∠EDF=90°,设运动时间为t秒.
①点D的坐标是 (用含t的代数式表示);
②当直线BC与△DEF有交点时,请求出t的取值范围;
(3)如图2,点P是△ABC内一动点,BP=![]() ,点M,N分别是AB,BC边上的两个动点,当△PMN的周长最小时,请直接写出四边形PNBM面积的最大值.
,点M,N分别是AB,BC边上的两个动点,当△PMN的周长最小时,请直接写出四边形PNBM面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,AD与BC相交于点E,AF平分∠BAD,交BC于点F,交CD的延长线于点G.

(1)若∠G=29°,求∠ADC的度数;
(2)若点F是BC的中点,求证:AB=AD+CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(抗击疫情)为了遏制新型冠状病毒疫情的蔓延势头,各地教育部门在推迟各级学校开学时间的同时提出“听课不停学”的要求,各地学校也都开展了远程网络教学,某校集中为学生提供四类在线学习方式:在线阅读、在线听课、在线答疑、在线讨论,为了了解学生的需求,该校通过网络对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查,并根据结果绘制成如下两幅不完整的统计图。

(1)本次调查的人数有多少人?
(2)请补全条形图;
(3)请求出“在线答疑”在扇形图中的圆心角度数;
(4)小宁和小娟都参加了远程网络教学活动,请求出小宁和小娟选择同一种学习方式的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com