
【题目】如图,![]() 是半圆
是半圆![]() 的直径,点
的直径,点![]() 是半圆上的一个动点,
是半圆上的一个动点,![]() 的角平分线交圆弧于点
的角平分线交圆弧于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() .
.
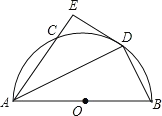
(1)求证:![]() 是半圆
是半圆![]() 的切线;
的切线;
(2)填空:①若![]() ,则
,则![]() __________;
__________;
②连接![]() 、
、![]() ,当
,当![]() 的度数为__________时,四边形
的度数为__________时,四边形![]() 是菱形.
是菱形.
【答案】(1)详见解析;(2)①2;②![]()
【解析】
(1)连接OD,根据角平分线的定义和已知以及平行线的判定得到OD∥AE,即∠ODE=∠E=90,即可证明;
(2)①作DG⊥AB于G,根据相似三角形的面积比等于相似比的平方求出△ADE与△ABD的面积比,根据三角形的面积公式计算即可;②根据菱形的判定定理和等边三角形的性质解答即.
(1)证明:如图1,连接OD
∵AD是∠BAC的角平分线,
∴∠EAD=∠DAB,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠EAD=∠ODA,
∴OD∥AE,![]()
∴∠ODE=∠E=90°
∴![]() 是半圆
是半圆![]() 的切线;
的切线;

(2)①如图2,作DG⊥AB于G
∵AD是∠BAC的角平分线,∠E=90°,DG⊥AB,
∴DE=DG,∠EAD=∠DAB,
∵∠ODE=∠E=90°,
∵△ADE∽△ABD,
∵![]()
∴△ADE与△ABD的面积比为3:4,即
∴AE:AB=3:4;

②如图3,当四边形BDCO是天菱形时,
∴BD=OC=CD=OB,CD∥OB,
当CD∥OB时,BD=AC
∴△AOC为等边三角形
∴当∠BAC=60°时,四边形BDCO是菱形.
故答案为:①3:4;②60°.



科目:初中数学 来源: 题型:
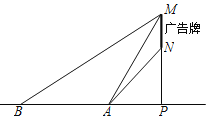
【题目】某数学社团成员想利用所学的知识测量某广告牌的宽度![]() 图中线段MN的长
图中线段MN的长![]() ,直线MN垂直于地面,垂足为点
,直线MN垂直于地面,垂足为点![]() 在地面A处测得点M的仰角为
在地面A处测得点M的仰角为![]() 、点N的仰角为
、点N的仰角为![]() ,在B处测得点M的仰角为
,在B处测得点M的仰角为![]() ,
,![]() 米,且A、B、P三点在一直线上
米,且A、B、P三点在一直线上![]() 请根据以上数据求广告牌的宽MN的长.
请根据以上数据求广告牌的宽MN的长.
![]() 参考数据:
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了做好新冠肺炎疫情期间开学工作,我区某中学用药熏消毒法对教室进行消毒.已知一瓶药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例;药物释放完毕后,y与x成反比例,如图所示.根据图中提供的信息,解答下列问题:
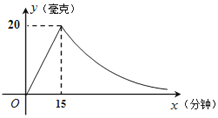
(1)写出倾倒一瓶药物后,从药物释放开始,y与x之间的两个函数关系式及相应的自变量取值范围;
(2)据测定,当空气中每立方米的含药量不低于8毫克时,消毒有效,那么倾倒一瓶药物后,从药物释放开始,有效消毒时间是多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(11·湖州)(本小题10分)
如图,已知E、F分别是□ABCD的边BC、AD上的点,且BE=DF。
⑴求证:四边形AECF是平行四边形;
⑵若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
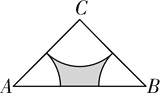
【题目】(2011贵州安顺)如图,在Rt△ABC中,∠C=90°,CA=CB=4,分别以A、B、C为圆心,以![]() AC为半径画弧,三条弧与边AB所围成的阴影部分的面积是 .
AC为半径画弧,三条弧与边AB所围成的阴影部分的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 的顶点为
的顶点为![]() ,与
,与![]() 轴的一个交点
轴的一个交点![]() 在点
在点![]() 和
和![]() 之间,其部分图象如图所示,则以下结论:①
之间,其部分图象如图所示,则以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④方程以
;④方程以![]() 有两个的实根,其中正确的个数为( )
有两个的实根,其中正确的个数为( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某区初中学生对网络游戏的喜好和作业量多少情况,随机抽取了该区500名同学进行了调查,并将调查的情况进行了整理,如下表:
作业量多少 网络游戏的喜好 | 认为作业多 | 认为作业不多 | 合计 |
喜欢网络游戏 | 180 | 90 | 270 |
不喜欢网络游戏 | 80 | 150 | 230 |
根据抽样调查结果,估计该区12000名初中生“不喜欢网络游戏并认为作业不多”的人数是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
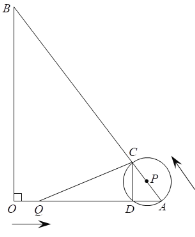
【题目】如图,在△AOB中,∠AOB=90°,OA=6,OB=8,动点Q从点O出发,沿着OA方向以1个单位长度/秒的速度匀速运动,同时动点P从点A出发,沿着AB方向也以1个单位长度/秒的速度匀速运动,设运动时间为t秒(0<t≤5),以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连结CD、CQ.
⑴ 当点Q与点D重合时,求t的值;
⑵ 若△ACQ是等腰三角形,求t的值;
⑶ 若⊙P与线段QC只有一个公共点,求t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+2(a<0)与x轴交于点A(﹣1,0)和点B(2,0),与y轴交于点C.
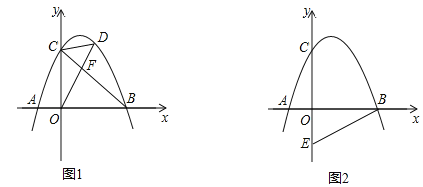
(1)求该抛物线的函数解析式;
(2)如图1,连接BC,点D是直线BC上方抛物线上的点,连接OD、CD,OD交BC于点F,当S△COF:S△CDF=2:1时,求点D的坐标;
(3)如图2,点E的坐标为(0,﹣1),在抛物线上是否存在点P,使∠OBP=2∠OBE?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com