
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпyЃНax2+bx+2ЃЈaЃМ0ЃЉгыxжсНЛгкЕуAЃЈЉ1ЃЌ0ЃЉКЭЕуBЃЈ2ЃЌ0ЃЉЃЌгыyжсНЛгкЕуCЃЎ
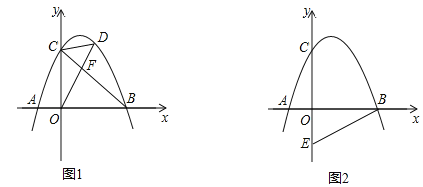
ЃЈ1ЃЉЧѓИУХзЮяЯпЕФКЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌСЌНгBCЃЌЕуDЪЧжБЯпBCЩЯЗНХзЮяЯпЩЯЕФЕуЃЌСЌНгODЁЂCDЃЌODНЛBCгкЕуFЃЌЕБSЁїCOFЃКSЁїCDFЃН2ЃК1ЪБЃЌЧѓЕуDЕФзјБъЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌЕуEЕФзјБъЮЊЃЈ0ЃЌЉ1ЃЉЃЌдкХзЮяЯпЩЯЪЧЗёДцдкЕуPЃЌЪЙЁЯOBPЃН2ЁЯOBEЃПШєДцдкЃЌЧыжБНгаДГіЗћКЯЬѕМўЕФЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉyЃНЉx2+x+2ЃЛЃЈ2ЃЉDЃЈ1ЃЌ2ЃЉЃЛЃЈ3ЃЉЃЈ![]() ЃЉЛђЃЈЉ
ЃЉЛђЃЈЉ![]() ЃЉЃЎ
ЃЉЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУД§ЖЈЯЕЪ§ЗЈЧѓНтЮіЪНМДПЩЕУЕНД№АИЃЌ
ЃЈ2ЃЉЙ§ЕуDзїDHЁЮyжсНЛBCгкЕуHЃЌНЛxжсгкЕуGЃЌРћгУSЁїCOFЃКSЁїCDFЃН2ЃК1ЕУЕНOFЃКDFЃН2ЃК1ЃЌРћгУЯрЫЦШ§НЧаЮЕФаджЪПЩЕУД№АИЃЌ
ЃЈ3ЃЉЗжЧщПіЬжТлЃКЂйЕБЕуPдкxжсЩЯЗНЪБЃЌдкyжсЩЯШЁЕуGЃЈ1ЃЌ0ЃЉЃЌСЌНгBGЃЌдђЁЯOBGЃНЁЯOBEЃЌЙ§ЕуBзїжБЯпPBНЛХзЮяЯпгкЕуPЃЌНЛyжсгкЕуMЃЌЪЙЁЯGBMЃНЁЯGBOЃЌдђЁЯOBPЃН2ЁЯOBEЃЌШЛКѓЧѓНт![]() ЕФНтЮіЪНЃЌНЈСЂЗНГЬзщЧѓНтМДПЩЃЌ
ЕФНтЮіЪНЃЌНЈСЂЗНГЬзщЧѓНтМДПЩЃЌ
ЂкЕБЕуPдкxжсЯТЗНЪБЃЌзїЕуMЃЈ0ЃЌ![]() ЃЉЙигкxжсЕФЖдГЦЕуNЃЈ0ЃЌ
ЃЉЙигкxжсЕФЖдГЦЕуNЃЈ0ЃЌ![]() ЃЉЃЌЧѓНт
ЃЉЃЌЧѓНт![]() ЕФНтЮіЪНЃЌНЈСЂЗНГЬзщЧѓНтМДПЩЃЎ
ЕФНтЮіЪНЃЌНЈСЂЗНГЬзщЧѓНтМДПЩЃЎ
НтЃКЃЈ1ЃЉЁпAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ2ЃЌ0ЃЉЃЌ
ЁрАбAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ2ЃЌ0ЃЉДњШыyЃНax2+bx+2ЕУЃЌ
![]()
НтЕУЃЌ![]()
ЁрИУХзЮяЯпЕФКЏЪ§НтЮіЪНЮЊyЃНЉx2+x+2ЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌЙ§ЕуDзїDHЁЮyжсНЛBCгкЕуHЃЌНЛxжсгкЕуGЃЌ
ЁпХзЮяЯпyЃНЉx2+x+2гыyжсНЛгкЕуCЃЌ
ЁрCЃЈ0ЃЌ2ЃЉЃЌ
ЩшжБЯпBCНтЮіЪНЮЊyЃНkx+bЃЌ
дђ![]() НтЕУ
НтЕУ![]()
ЁржБЯпBCНтЮіЪНЮЊyЃНЉx+2ЃЌ
ЁпSЁїCOFЃКSЁїCDFЃН2ЃК1ЃЌ
ЁрOFЃКDFЃН2ЃК1ЃЌ
ЁпDHЁЮOCЃЌ
ЁрЁїOFCЁзЁїDFHЃЌ
Ёр![]()
ЁрOCЃН2DHЃЌ
ЩшDЃЈaЃЌЉa2+a+2ЃЉЃЌдђHЃЈaЃЌЉa+2ЃЉЃЌ
ЁрDHЃНЉa2+a+2ЉЃЈЉa+2ЃЉЃНЉa2+2aЃЌ
Ёр2ЃН2ЃЈЉa2+2aЃЉЃЌ
НтЕУaЃН1ЃЌ
ЁрDЃЈ1ЃЌ2ЃЉЃЎ
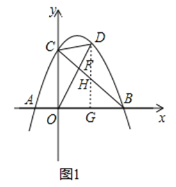
ЃЈ3ЃЉЂйЕБЕуPдкxжсЩЯЗНЪБЃЌ
дкyжсЩЯШЁЕуGЃЈ1ЃЌ0ЃЉЃЌСЌНгBGЃЌдђЁЯOBGЃНЁЯOBEЃЌЙ§ЕуBзїжБЯпPBНЛХзЮяЯпгкЕуPЃЌНЛyжсгкЕуMЃЌЪЙЁЯGBMЃНЁЯGBOЃЌ
дђЁЯOBPЃН2ЁЯOBEЃЌ
Й§ЕуGзїGHЁЭBMЃЌ
ЁпEЃЈ0ЃЌЉ1ЃЉЃЌ
ЁрOEЃНOGЃНGHЃН1ЃЌ
ЩшMHЃНxЃЌдђMGЃН![]() ЃЌ
ЃЌ
дкRtЁїOBMжаЃЌOB2+OM2ЃНMB2ЃЌ
ЁрЃЈ![]() +1ЃЉ2+4ЃНЃЈx+2ЃЉ2ЃЌ
+1ЃЉ2+4ЃНЃЈx+2ЃЉ2ЃЌ
НтЕУЃКxЃН![]() ЃЌ
ЃЌ![]() ЃЈЩсШЅЃЉ
ЃЈЩсШЅЃЉ
ЙЪMGЃН![]() ЃН
ЃН![]()
ЁрOMЃНOG+MGЃН![]()
ЁрЕуMЃЈ0ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
НЋЕуBЃЈ2ЃЌ0ЃЉЁЂMЃЈ0ЃЌ![]() ЃЉЕФзјБъДњШывЛДЮКЏЪ§БэДяЪНyЃНmx+nЃЌ
ЃЉЕФзјБъДњШывЛДЮКЏЪ§БэДяЪНyЃНmx+nЃЌ
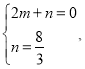
НтЕУЃК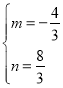 ЃЌ
ЃЌ
ЁржБЯпBMЕФБэДяЪНЮЊЃК![]()
Ёр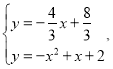
НтЕУЃК![]() ЛђxЃН2ЃЈЩсШЅЃЉЃЌ
ЛђxЃН2ЃЈЩсШЅЃЉЃЌ
ЁрЕуP![]() ЃЛ
ЃЛ
ЂкЕБЕуPдкxжсЯТЗНЪБЃЌ
зїЕуMЃЈ0ЃЌ![]() ЃЉЙигкxжсЕФЖдГЦЕуNЃЈ0ЃЌ
ЃЉЙигкxжсЕФЖдГЦЕуNЃЈ0ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЭЌРэПЩЕУЃК
жБЯпBNЕФНтЮіЪНЮЊ![]()
Ёр
НтЕУЃЌ![]() ЛђxЃН2ЃЈЩсШЅЃЉЃЌ
ЛђxЃН2ЃЈЩсШЅЃЉЃЌ
ЁрЕуP![]() ЃЛ
ЃЛ
злКЯвдЩЯПЩЕУЃЌЕуPЕФзјБъЮЊ![]() Лђ
Лђ![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() ЪЧАыдВ
ЪЧАыдВ![]() ЕФжБОЖЃЌЕу
ЕФжБОЖЃЌЕу![]() ЪЧАыдВЩЯЕФвЛИіЖЏЕуЃЌ
ЪЧАыдВЩЯЕФвЛИіЖЏЕуЃЌ![]() ЕФНЧЦНЗжЯпНЛдВЛЁгкЕу
ЕФНЧЦНЗжЯпНЛдВЛЁгкЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() гкЕу
гкЕу![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓжЄЃК![]() ЪЧАыдВ
ЪЧАыдВ![]() ЕФЧаЯпЃЛ
ЕФЧаЯпЃЛ
ЃЈ2ЃЉЬюПеЃКЂйШє![]() ЃЌдђ
ЃЌдђ![]() __________ЃЛ
__________ЃЛ
ЂкСЌНг![]() ЁЂ
ЁЂ![]() ЃЌЕБ
ЃЌЕБ![]() ЕФЖШЪ§ЮЊ__________ЪБЃЌЫФБпаЮ
ЕФЖШЪ§ЮЊ__________ЪБЃЌЫФБпаЮ![]() ЪЧСтаЮЃЎ
ЪЧСтаЮЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпyЃНax2+bx+![]() гыxжсЗжБ№НЛгкЕуAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉЃЌЕуCЪЧЖЅЕуЃЎ
гыxжсЗжБ№НЛгкЕуAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉЃЌЕуCЪЧЖЅЕуЃЎ
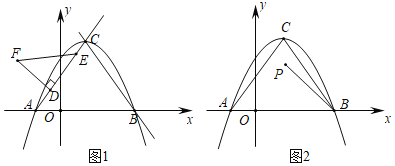
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌЯпЖЮDEЪЧЩфЯпACЩЯЕФвЛЬѕЖЏЯпЖЮЃЈЕуDдкЕуEЕФЯТЗНЃЉЃЌЧвDEЃН2ЃЌЕуDДгЕуAГіЗЂбизХЩфЯпACЕФЗНЯђвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШдЫЖЏЃЌвдDEЮЊвЛБпдкACЩЯЗНзїЕШбќRtЁїDEFЃЌЦфжаЁЯEDFЃН90ЁуЃЌЩшдЫЖЏЪБМфЮЊtУыЃЎ
ЂйЕуDЕФзјБъЪЧЁЁ ЁЁЃЈгУКЌtЕФДњЪ§ЪНБэЪОЃЉЃЛ
ЂкЕБжБЯпBCгыЁїDEFгаНЛЕуЪБЃЌЧыЧѓГіtЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌЕуPЪЧЁїABCФквЛЖЏЕуЃЌBPЃН![]() ЃЌЕуMЃЌNЗжБ№ЪЧABЃЌBCБпЩЯЕФСНИіЖЏЕуЃЌЕБЁїPMNЕФжмГЄзюаЁЪБЃЌЧыжБНгаДГіЫФБпаЮPNBMУцЛ§ЕФзюДѓжЕЃЎ
ЃЌЕуMЃЌNЗжБ№ЪЧABЃЌBCБпЩЯЕФСНИіЖЏЕуЃЌЕБЁїPMNЕФжмГЄзюаЁЪБЃЌЧыжБНгаДГіЫФБпаЮPNBMУцЛ§ЕФзюДѓжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
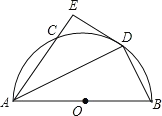
ЁОЬтФПЁПШчЭМЃЌABЁЮCDЃЌADгыBCЯрНЛгкЕуEЃЌAFЦНЗжЁЯBADЃЌНЛBCгкЕуFЃЌНЛCDЕФбгГЄЯпгкЕуGЃЎ

ЃЈ1ЃЉШєЁЯG=29ЁуЃЌЧѓЁЯADCЕФЖШЪ§ЃЛ
ЃЈ2ЃЉШєЕуFЪЧBCЕФжаЕуЃЌЧѓжЄЃКAB=AD+CDЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖўДЮКЏЪ§yЃНax2+bx+cЃЈaЁй0ЃЉЕФЭМЯѓШчЭМЫљЪОЃЌЦфЖдГЦжсЮЊжБЯпxЃНЉ1ЃЌгыxжсЕФНЛЕуЮЊ(x1ЃЌ0)ЁЂ(x2ЃЌ0)ЃЌЦфжа0ЃМx2ЃМ1ЃЌгаЯТСаНсТлЃКЂйb2Љ4acЃО0ЃЛЂк4aЉ2b+cЃОЉ1ЃЛЂлЉ3ЃМx1ЃМЉ2ЃЛЂмЕБmЮЊШЮвтЪЕЪ§ЪБЃЌaЉbЁмam2+bmЃЛЂн3a+cЃН0ЃЎЦфжаЃЌе§ШЗЕФНсТлгаЃЈ ЃЉ
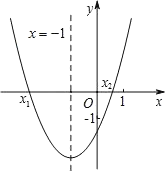
A.ЂкЂлЂмB.ЂйЂлЂнC.ЂкЂмЂнD.ЂйЂлЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊТфЪЕЙњЮёдКЗПЕиВњЕїПиеўВпЃЌЪЙЁАОгепгаЦфЮнЁБЃЌФГЪаМгПьСЫСЎзтЗПЕФНЈЩшСІЖШЃЎ2015ФъЪаеўИЎЙВЭЖзЪ3вкдЊШЫУёБвНЈЩшСЫСЎзтЗП12ЭђЦНЗНУзЃЌ2017ФъМЦЛЎЭЖзЪ6.75вкдЊШЫУёБвНЈЩшСЎзтЗПЃЌШєдкетСНФъФкУПФъЭЖзЪЕФдіГЄТЪЯрЭЌЃЎ
(1)ЧѓУПФъЪаеўИЎЭЖзЪЕФдіГЄТЪЃЛ
(2)ШєетСНФъФкЕФНЈЩшГЩБОВЛБфЃЌЮЪДг2015ЕН2017ФъетШ§ФъЙВНЈЩшСЫЖрЩйЭђЦНЗНУзСЎзтЗПЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПга4еХЯрЭЌЕФПЈЦЌЗжБ№аДзХЪ§зжЉ1ЁЂ2ЁЂЉ3ЁЂ4ЃЌНЋПЈЦЌЕФБГУцГЏЩЯЃЌВЂЯДдШЃЎДгжаШЮвтГщШЁ1еХЃЌВЂНЋЫљШЁПЈЦЌЩЯЕФЪ§зжМЧзївЛДЮКЏЪ§y=kx+bжаЕФkЃЛдйДггрЯТЕФПЈЦЌжаШЮвтГщШЁ1еХЃЌВЂНЋЫљШЁПЈЦЌЩЯЕФЪ§зжМЧзївЛДЮКЏЪ§y=kx+bжаЕФbЃЎдђетИівЛДЮКЏЪ§ЕФЭМЯѓЧЁКУОЙ§ЕквЛЁЂЖўЁЂЫФЯѓЯоЕФИХТЪЪЧ_______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈПЙЛївпЧщЃЉЮЊСЫЖєжЦаТаЭЙкзДВЁЖОвпЧщЕФТћбгЪЦЭЗЃЌИїЕиНЬг§ВПУХдкЭЦГйИїМЖбЇаЃПЊбЇЪБМфЕФЭЌЪБЬсГіЁАЬ§ПЮВЛЭЃбЇЁБЕФвЊЧѓЃЌИїЕибЇаЃвВЖМПЊеЙСЫдЖГЬЭјТчНЬбЇЃЌФГаЃМЏжаЮЊбЇЩњЬсЙЉЫФРрдкЯпбЇЯАЗНЪНЃКдкЯпдФЖСЁЂдкЯпЬ§ПЮЁЂдкЯпД№вЩЁЂдкЯпЬжТлЃЌЮЊСЫСЫНтбЇЩњЕФашЧѓЃЌИУаЃЭЈЙ§ЭјТчЖдБОаЃВПЗжбЇЩњНјааСЫЁАФуЖдФФРрдкЯпбЇЯАЗНЪНзюИааЫШЄЁБЕФЕїВщЃЌВЂИљОнНсЙћЛцжЦГЩШчЯТСНЗљВЛЭъећЕФЭГМЦЭМЁЃ

ЃЈ1ЃЉБОДЮЕїВщЕФШЫЪ§гаЖрЩйШЫЃП
ЃЈ2ЃЉЧыВЙШЋЬѕаЮЭМЃЛ
ЃЈ3ЃЉЧыЧѓГіЁАдкЯпД№вЩЁБдкЩШаЮЭМжаЕФдВаФНЧЖШЪ§ЃЛ
ЃЈ4ЃЉаЁФўКЭаЁОъЖМВЮМгСЫдЖГЬЭјТчНЬбЇЛюЖЏЃЌЧыЧѓГіаЁФўКЭаЁОъбЁдёЭЌвЛжжбЇЯАЗНЪНЕФИХТЪ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ2011ЩНЖЋМУФЯЃЌ27ЃЌ9ЗжЃЉШчЭМЃЌОиаЮOABCжаЃЌЕуOЮЊдЕуЃЌЕуAЕФзјБъЮЊЃЈ0ЃЌ8ЃЉЃЌЕуCЕФзјБъЮЊЃЈ6ЃЌ0ЃЉЃЎХзЮяЯп![]() ОЙ§AЁЂCСНЕуЃЌгыABБпНЛгкЕуDЃЎ
ОЙ§AЁЂCСНЕуЃЌгыABБпНЛгкЕуDЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉЕуPЮЊЯпЖЮBCЩЯвЛИіЖЏЕуЃЈВЛгыЕуCжиКЯЃЉЃЌЕуQЮЊЯпЖЮACЩЯвЛИіЖЏЕуЃЌAQ=CPЃЌСЌНгPQЃЌЩшCP=mЃЌЁїCPQЕФУцЛ§ЮЊSЃЎ
ЂйЧѓSЙигкmЕФКЏЪ§БэДяЪНЃЌВЂЧѓГіmЮЊКЮжЕЪБЃЌSШЁЕУзюДѓжЕЃЛ
ЂкЕБSзюДѓЪБЃЌдкХзЮяЯп![]() ЕФЖдГЦжсlЩЯШєДцдкЕуFЃЌЪЙЁїFDQЮЊжБНЧШ§НЧаЮЃЌЧыжБНгаДГіЫљгаЗћКЯЬѕМўЕФFЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФЖдГЦжсlЩЯШєДцдкЕуFЃЌЪЙЁїFDQЮЊжБНЧШ§НЧаЮЃЌЧыжБНгаДГіЫљгаЗћКЯЬѕМўЕФFЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ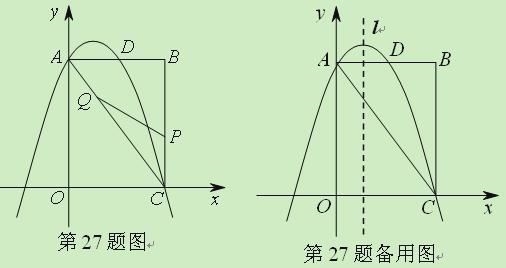
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com