
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为直线x=﹣1,与x轴的交点为(x1,0)、(x2,0),其中0<x2<1,有下列结论:①b2﹣4ac>0;②4a﹣2b+c>﹣1;③﹣3<x1<﹣2;④当m为任意实数时,a﹣b≤am2+bm;⑤3a+c=0.其中,正确的结论有( )
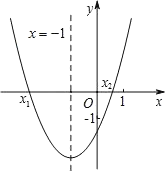
A.②③④B.①③⑤C.②④⑤D.①③④
【答案】D
【解析】
根据函数图象和二次函数的性质,可以判断各个小题中的结论是否成立,本题得以解决.
∵二次函数y=ax2+bx+c(a≠0)的图象与x轴有两个交点,
∴b2-4ac>0,故①正确;
∵该函数图象的对称轴是x=-1,当x=0时的函数值小于-1,
∴x=-2时的函数值和x=0时的函数值相等,都小于-1,
∴4a-2b+c<-1,故②错误;
∵该函数图象的对称轴是x=-1,与x轴的交点为(x1,0)、(x2,0),其中0<x2<1,
∴-3<x,1<-2,故③正确;
∵当x=-1时,该函数取得最小值,
∴当m为任意实数时,a-b≤am2+bm,故④正确;
∵-![]() =-1,
=-1,
∴b=2a,
∵x=1时,y=a+b+c>0,
∴3a+c>0,故⑤错误;
故选:D.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
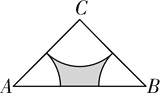
【题目】(2011贵州安顺)如图,在Rt△ABC中,∠C=90°,CA=CB=4,分别以A、B、C为圆心,以![]() AC为半径画弧,三条弧与边AB所围成的阴影部分的面积是 .
AC为半径画弧,三条弧与边AB所围成的阴影部分的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
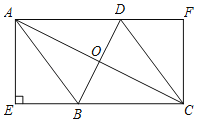
【题目】如图,在菱形ABCD中,对角线AC,BD交于点O,AE⊥BC交CB延长线于点E,CF∥AE交AD延长线于点F.
(1)求证:四边形AECF是矩形;
(2)连接OE,若AE=12,AD=13,则线段OE的长度是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数![]() 的图象经过点(
的图象经过点(![]() ,
,![]() )和(
)和(![]() ,
,![]() ),完成下面问题:
),完成下面问题:
(1)求函数![]() 的表达式;
的表达式;
(2)在给出的平面直角坐标系中,请用适当的方法画出这个函数的图象,并写出这个函数的一条性质;

(3)已知函数![]() 的图象如图所示,结合你所画出
的图象如图所示,结合你所画出![]() 的图象,直接写出
的图象,直接写出![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+2(a<0)与x轴交于点A(﹣1,0)和点B(2,0),与y轴交于点C.
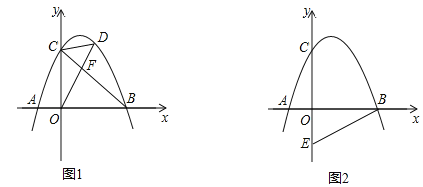
(1)求该抛物线的函数解析式;
(2)如图1,连接BC,点D是直线BC上方抛物线上的点,连接OD、CD,OD交BC于点F,当S△COF:S△CDF=2:1时,求点D的坐标;
(3)如图2,点E的坐标为(0,﹣1),在抛物线上是否存在点P,使∠OBP=2∠OBE?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小学学生较多,为了便于学生尽快就餐,师生约定:早餐一人一份,一份两样,一样一个,食堂师傅在窗口随机发放(发放的食品价格一样),食堂在某天早餐提供了猪肉包、面包、鸡蛋、油饼四样食品.
(1)按约定,“小李同学在该天早餐得到两个油饼”是 事件;(可能,必然,不可能)
(2)请用列表或树状图的方法,求出小张同学该天早餐刚好得到猪肉包和油饼的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
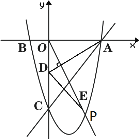
【题目】如图,抛物线![]() 经过点A(3,0),B(
经过点A(3,0),B(![]() ,0),与y轴交于点C,点P是抛物线在第四象限内的一点.
,0),与y轴交于点C,点P是抛物线在第四象限内的一点.
(1)求抛物线解析式;
(2)点D是线段OC的中点,OP⊥AD,点E是射线OP上一点,OE=AD,求DE的长;
(3)连接CP,AP,是否存在点P,使得OP平分四边形ABCP的面积?若存在,求点P的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 已知点P为⊙O 外一点,PA、PB是⊙O的切线,切点分别是A、B,连接OP交AB于点C,交⊙O于点D,若PA=3cm, ∠APB=60°,则下列结论正确的有( )
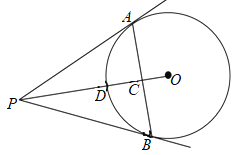
①AB⊥OP;②AC2=PC·OC;③若连接AD,BD,则∠ADB=120°;④PA,PB与劣弧AB围成的图形的面积是![]()
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com