
【题目】如图,AB∥CD,AD与BC相交于点E,AF平分∠BAD,交BC于点F,交CD的延长线于点G.

(1)若∠G=29°,求∠ADC的度数;
(2)若点F是BC的中点,求证:AB=AD+CD.
【答案】(1)58°;(2)详见解析
【解析】
(1)根据平行和角平分线,可推导出∠ADC=2∠G,从而得出∠ADC的大小;
(2)证△ABF≌△GCF,从而得出AB=GC,从而证AB=AD+CD.
证明:(1)∵AB∥CD,∴ ∠BAG=∠G, ∠BAD=∠ADC.
∵AF平分∠BAD,∴∠BAD=2∠BAG=2∠G.
∴∠ADC=∠BAD=2∠G .
∵∠G=29°,∴∠ADC=58°.
(2)∵AF平分∠BAD,∴∠BAG=∠DAG.
∵∠BAG=∠G, ∴∠DAG=∠G.
∴AD=GD.
∵点F是BC的中点,∴BF=CF.
在△ABF和△GCF中,
∵
∴△ABF≌△GCF.
∴AB=GC.
∴AB=GD+CD=AD+CD.


科目:初中数学 来源: 题型:
【题目】(11·湖州)(本小题10分)
如图,已知E、F分别是□ABCD的边BC、AD上的点,且BE=DF。
⑴求证:四边形AECF是平行四边形;
⑵若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
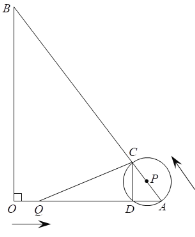
【题目】如图,在△AOB中,∠AOB=90°,OA=6,OB=8,动点Q从点O出发,沿着OA方向以1个单位长度/秒的速度匀速运动,同时动点P从点A出发,沿着AB方向也以1个单位长度/秒的速度匀速运动,设运动时间为t秒(0<t≤5),以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连结CD、CQ.
⑴ 当点Q与点D重合时,求t的值;
⑵ 若△ACQ是等腰三角形,求t的值;
⑶ 若⊙P与线段QC只有一个公共点,求t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图1是儿童写字支架示意图,由一面黑板,一面白板和一块固定支架的托盘组成,图2是它的一个左侧截面图,该支架是个轴对称图形,∠BAC是可以转动的角,B,C、D,E和F,G是支架腰上的三对对称点,是用来卡住托盘以固定支架的。已知AB=AC=60cm,BD=CE=DF=EG=10cm。
(1)当托盘固定在BC处时,∠BAC=32,求托盘BC的长;(精确到0.1)
(2)当托盘固定在DE处时,这是儿童看支架的最佳角度,求此时∠BAC的度数。
(参考数据:sin32=0.53,cos32=0.85,sin16=0.28
sin20=0.34,sin25=0.42。)


图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系内,点A,B的坐标分别为(1,0),(0,2),AC⊥AB,且AB=AC,直线BC交![]() 轴于点D,抛物线
轴于点D,抛物线![]() 经过点A,B,D.
经过点A,B,D.

(1)求直线BC和抛物线![]() 的函数表达式;
的函数表达式;
(2)点P是直线BD下方的抛物线上一点,求△PCD面积的最大值,以及△PCD面积取得最大值时,点P的坐标;
(3)若点P的坐标为(2)小题中,△PCD的面积取得最大值时对应的坐标.平面内存在直线l,使点B,D,P到该直线的距离都相等,请直接写出所有满足条件的直线l的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+2(a<0)与x轴交于点A(﹣1,0)和点B(2,0),与y轴交于点C.
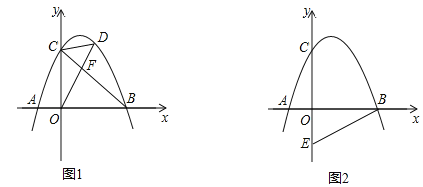
(1)求该抛物线的函数解析式;
(2)如图1,连接BC,点D是直线BC上方抛物线上的点,连接OD、CD,OD交BC于点F,当S△COF:S△CDF=2:1时,求点D的坐标;
(3)如图2,点E的坐标为(0,﹣1),在抛物线上是否存在点P,使∠OBP=2∠OBE?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市在疫情期间购进一批含75%酒精的消毒湿巾投放市场,则开始,由于消费者对此类产品认识不足,前几天的销量每况愈下;为了打开市场,提高销量,超市决定对该消毒湿巾打折销售,日销量每日增加,时间每增加1天,则日销量增加20包.超市工作人员对一个月(30天)销售情况进行了跟踪记录,并将记录情况绘成图像,图中的折线ABC表示该消毒湿巾日销量y(包)与销售时间x(天)之间的函数关系;
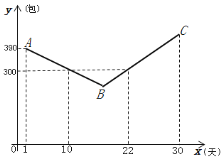
(1)第28天的日销售量是_______包;
(2)求y与x之间的函数关系式,并写出x的取值范围;
(3)若该产口进价为5元/包,AB段售价为15元/包,BC段在15元/包的基础上打a折销售,并且在30天中利润不低于3400元的天数有且只有10天,试确定a的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,△ABC中,∠C>∠B.
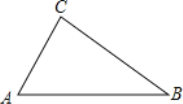
(1)尺规作图:作∠ACM=∠B,且使CM与边AB交于点D(保留作图痕迹,不写作法和证明);
(2)在(1)中所形成的图形中,若AD=2,BD=4,求AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com