
【题目】随着![]() 技术的发展,人们对各类
技术的发展,人们对各类![]() 产品的使用充满期待.某公司计划在某地区销售第一款
产品的使用充满期待.某公司计划在某地区销售第一款![]() 产品,根据市场分析,该产品的销售价格将随销售周期的变化而变化.设该产品在第
产品,根据市场分析,该产品的销售价格将随销售周期的变化而变化.设该产品在第![]() (
(![]() 为正整数)个销售周期每台的销售价格为
为正整数)个销售周期每台的销售价格为![]() 元,
元,![]() 与
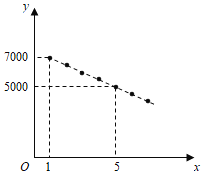
与![]() 之间满足如图所示的一次函数关系.
之间满足如图所示的一次函数关系.
(1)求![]() 与
与![]() 之间的关系式;
之间的关系式;
(2)设该产品在第![]() 个销售周期的销售数量为
个销售周期的销售数量为![]() (万台),
(万台),![]() 与
与![]() 的关系可用
的关系可用![]() 来描述.根据以上信息,试问:哪个销售周期的销售收入最大?此时该产品每台的销售价格是多少元?
来描述.根据以上信息,试问:哪个销售周期的销售收入最大?此时该产品每台的销售价格是多少元?
科目:初中数学 来源: 题型:
【题目】随着中国经济的快速发展以及科技水平的飞速提高,中国高铁正迅速崛起.高铁大大缩短了时空距离,改变了人们的出行方式.如图,![]() ,
,![]() 两地被大山阻隔,由
两地被大山阻隔,由![]() 地到
地到![]() 地需要绕行
地需要绕行![]() 地,若打通穿山隧道,建成
地,若打通穿山隧道,建成![]() ,
,![]() 两地的直达高铁,可以缩短从
两地的直达高铁,可以缩短从![]() 地到
地到![]() 地的路程.已知:
地的路程.已知:![]() ,
,![]() ,
,![]() 公里,求隧道打通后与打通前相比,从
公里,求隧道打通后与打通前相比,从![]() 地到
地到![]() 地的路程将约缩短多少公里?(参考数据:
地的路程将约缩短多少公里?(参考数据:![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索规律:观察下面由组成的图案和算式,解答问题:
1+3=4=22
1+3+5=9=32
1+3+5+7=16=42
1+3+5+7+9=25=52
(1)请计算 1+3+5+7+9+11;
(2)请计算 1+3+5+7+9+…+19;
(3)请计算 1+3+5+7+9+…+(2n﹣1);
(4)请用上述规律计算:21+23+25+…+99.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一次函数y=px+q的特征数为[p,q].如:y=3x-1的特征数是[3,-1]
(1)若某正比例函数的特征数是[k+2, ![]() ],求k的值.
],求k的值.
(2)在平面直角坐标系中,有两点A(-m,0),B(0,-2m),且△OAB的面积为4(O为原点),求过A、B两点的一次函数的特征数.
查看答案和解析>>
科目:初中数学 来源: 题型:
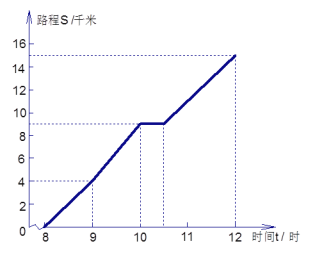
【题目】图为一位旅行者在早晨8时从城市出发到郊外所走的路程S(单位:千米)与时间t(单位:时)的变量关系的图象.根据图象回答问题:
(1)在这个变化过程中,自变量是________,因变量是________.
(2)9时,10时,所走的路程分别是多少?
(3)他休息了多长时间?
(4)他从休息后直至到达目的地这段时间的平均速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市预测某饮料有发展前途,用1600元购进一批饮料,面市后果然供不应求,又用6000元购进这批饮料,第二批饮料的数量是第一批的3倍,但单价比第一批贵2元.
(1)第一批饮料进货单价多少元?
(2)若二次购进饮料按同一价格销售,两批全部售完后,获利不少于1200元,那么销售单价至少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高速公路养护小组乘车沿南北公路巡视维护,如果约定向北为正,向南为负,当天的行驶记录如下(单位:千米)+17,-9,+7,-15,+10,-8,+16.
(1)养护小组最后到达的地方在出发点的哪个方向?距离出发点多远?
(2)若汽车耗油量为0.3升/千米,则这次养护共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
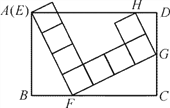
【题目】如图,由8个大小相等的小正方形构成的图案,它的四个顶点 E,F,G,H分别在矩形ABCD的边AB,BC,CD,DA上,若AB=4,BC=6,则DG的长是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com