
【题目】如图①,在![]() 中,
中,![]() 平分
平分![]() (
(![]() ),
),![]() 为
为![]() 上一点,且
上一点,且![]() 于点
于点![]() .
.
(1)当![]() ,
,![]() 时,求
时,求![]() 的度数;
的度数;
(2)若![]() ,
,![]() ,请结合(1)的计算猜想
,请结合(1)的计算猜想![]() 、
、![]() 、
、![]() 之间的数量关系,直接写出答案,不说明理由;(用含有
之间的数量关系,直接写出答案,不说明理由;(用含有![]() 、
、![]() 的式子表示
的式子表示![]() )
)
(3)如图②,当点![]() 在
在![]() 的延长线上时,其余条件不变,则(2)中的结论还成立吗?若成立,请说明为什么;若不成立,请写出成立的结论,并说明为什么.
的延长线上时,其余条件不变,则(2)中的结论还成立吗?若成立,请说明为什么;若不成立,请写出成立的结论,并说明为什么.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)成立.
;(3)成立. ![]() ,理由见解析.
,理由见解析.
【解析】
(1)根据三角形的内角和定理求出∠BAC,再根据角平分线的定义求出∠BAE,然后根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解;
(2)根据三角形的内角和定理和角平分线的定义表示出∠BAE,再根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠AEC,然后根据直角三角形两锐角互余列式整理即可得解;
(3)结论仍然成立.根据(2)可以得到∠AEC=90°+![]() (∠B-∠C),根据对顶角相等即可求得∠DEF,然后利用直角三角形的两个锐角互余即可求解.
(∠B-∠C),根据对顶角相等即可求得∠DEF,然后利用直角三角形的两个锐角互余即可求解.
(1)∵![]() ,
,![]() (已知)
(已知)
![]() (三角形的内角和等于
(三角形的内角和等于![]() )
)
∴![]() (等量代换)
(等量代换)
![]()
∵![]() 平分
平分![]() (已知)
(已知)
∴![]() (角平分线的定义)
(角平分线的定义)
∴![]() (三角形的一个外角等于和它不相邻的两个内角的和)
(三角形的一个外角等于和它不相邻的两个内角的和)
![]() ,即
,即![]() .
.
∵![]() 于点
于点![]() (已知)
(已知)
∴![]() (垂直的定义)
(垂直的定义)
∴![]() (直角三角形的两个锐角互余)
(直角三角形的两个锐角互余)
∴![]() (等量代换)
(等量代换)
![]()
(2)![]()
(3)成立. ![]()
理由:∵![]() ,
,![]() (已知)
(已知)
![]() (三角形的内角和等于
(三角形的内角和等于![]() )
)
∴![]() (等量代换)
(等量代换)
∵![]() 平分
平分![]() (已知)
(已知)
∴![]() (角平分线的定义)
(角平分线的定义)
∴![]() (三角形的一个外角等于和它不相邻的两个内角的和)
(三角形的一个外角等于和它不相邻的两个内角的和)
![]()
∴![]() (对顶角相等)
(对顶角相等)
∵![]() 于点
于点![]() (已知)
(已知)
∴![]() (垂直的定义)
(垂直的定义)
∴![]() (直角三角形的两个锐角互余 )
(直角三角形的两个锐角互余 )
∴![]() (等量代换)
(等量代换)
![]()


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
【题目】如图,已知∠A=∠AGE,∠D=∠DGC
(1)求证:AB∥CD;
(2)若∠1+∠2=180°,求证:∠BEC+∠B=180°;
(3)在(2)的基础上,若∠BEC=2∠B+30°,求∠C的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程![]()
(1)求证:不论k取什么实数值,这个方程总有实数根;
(2)若等腰三角形ABC的一边长为![]() ,另两边的长b、c恰好是这个方程的两个根,求△ABC的周长.
,另两边的长b、c恰好是这个方程的两个根,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD是由六个正方形组成的完美长方形,中间最小正方形的面积是1,最大正方形的边长为x.

(1)用x的代数式表示长方形ABCD的长是______或______、宽是______;
(2)求长方形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
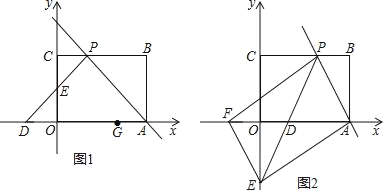
【题目】如图1,矩形OABC摆放在平面直角坐标系中,点A在x轴上,点C在y轴上,OA=3,OC=2,过点A的直线交矩形OABC的边BC于点P,且点P不与点B、C重合,过点P作∠CPD=∠APB,PD交x轴于点D,交y轴于点E.
(1)若△APD为等腰直角三角形.
①求直线AP的函数解析式;
②在x轴上另有一点G的坐标为(2,0),请在直线AP和y轴上分别找一点M、N,使△GMN的周长最小,并求出此时点N的坐标和△GMN周长的最小值.
(2)如图2,过点E作EF∥AP交x轴于点F,若以A、P、E、F为顶点的四边形是平行四边形,求直线PE的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】★若两个扇形满足弧长的比等于它们半径的比,则称这两个扇形相似.如图,如果扇形AOB与扇形A1O1B1是相似扇形,且半径OA∶O1A1=k(k为不等于0的常数).那么下面四个结论:①∠AOB=∠A1O1B1;②△AOB∽△A1O1B1;③![]() =k;④扇形AOB与扇形A1O1B1的面积之比为k2.成立的个数为( )
=k;④扇形AOB与扇形A1O1B1的面积之比为k2.成立的个数为( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线 AB∥CD,直线 a 分别交 AB、CD 于点 E、F,点 M 在线段 EF 上,点 P 是 直线 CD 上的一个动点(点 P 不与点 F 重合).
(1)如图 1,当点 P 在射线 FC 上移动时,∠FMP+∠FPM 与∠AEF 有什么数量关系? 请说明理由;
(2)如图 2,当点 P 在射线 FD 上移动时,∠FMP+∠FPM 与∠AEF 有什么数量关系? 请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
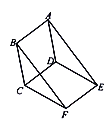
【题目】如图,已知平行四边形ABCD与平行四边形DCFE的周长相等,且![]() BAD=60°,
BAD=60°,![]() CFE=110°,则下列结论:①四边形ABFE为平行四边形;②
CFE=110°,则下列结论:①四边形ABFE为平行四边形;②![]() ADE是等腰三角形;③平行四边形ABCD与平行四边形DCFE全等;④
ADE是等腰三角形;③平行四边形ABCD与平行四边形DCFE全等;④![]() DAE=25°.其中正确的结论是.__________(填正确结论的序号)
DAE=25°.其中正确的结论是.__________(填正确结论的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com