
【题目】某公司计划从甲、乙两种产品中选择一种生产并销售,每年产销x件.已知产销两种产品的有关信息如表:

其中a为常数,且3≤a≤5.
(1)若产销甲、乙两种产品的年利润分别为![]() 万元、
万元、![]() 万元,直接写出
万元,直接写出![]() 、
、![]() 与x的函数关系式;
与x的函数关系式;
(2)分别求出产销两种产品的最大年利润;
(3)为获得最大年利润,该公司应该选择产销哪种产品?请说明理由.
【答案】(1)![]() =(6﹣a)x﹣20,(0<x≤200),
=(6﹣a)x﹣20,(0<x≤200),![]() .(0<x≤80);(2)
.(0<x≤80);(2)![]() 的值最大=(1180﹣200a)万元,
的值最大=(1180﹣200a)万元,![]() 最大值=440万元;(3)当a=3.7时,生产甲乙两种产品的利润相同;当3≤a<3.7时,生产甲产品利润比较高;当3.7<a≤5时,生产乙产品利润比较高.
最大值=440万元;(3)当a=3.7时,生产甲乙两种产品的利润相同;当3≤a<3.7时,生产甲产品利润比较高;当3.7<a≤5时,生产乙产品利润比较高.
【解析】
试题分析:(1)根据利润=销售数量×每件的利润即可解决问题.
(2)根据一次函数的增减性,二次函数的增减性即可解决问题.
(3)根据题意分三种情形分别求解即可:)①(1180﹣200a)=440,②(1180﹣200a)>440,③(1180﹣200a)<440.
试题解析:(1)![]() =(6﹣a)x﹣20,(0<x≤200);
=(6﹣a)x﹣20,(0<x≤200);
![]() ,即
,即![]() .(0<x≤80).
.(0<x≤80).
(2)对于![]() =(6﹣a)x﹣20,∵6﹣a>0,∴x=200时,
=(6﹣a)x﹣20,∵6﹣a>0,∴x=200时,![]() 的值最大=(1180﹣200a)万元.
的值最大=(1180﹣200a)万元.
对于![]() ,∵0<x≤80,∴x=80时,
,∵0<x≤80,∴x=80时,![]() 最大值=440万元.
最大值=440万元.
(3)①(1180﹣200a)=440,解得a=3.7,②(1180﹣200a)>440,解得a<3.7,③(1180﹣200a)<440,解得a>3.7,∵3≤a≤5,∴当a=3.7时,生产甲乙两种产品的利润相同;
当3≤a<3.7时,生产甲产品利润比较高;
当3.7<a≤5时,生产乙产品利润比较高.


科目:初中数学 来源: 题型:
【题目】若抛物线L:![]() (a,b,c是常数,abc≠0)与直线l都经过y轴上的一点P,且抛物线L的顶点Q在直线l上,则称此直线l与该抛物线L具有“一带一路”关系.此时,直线l叫做抛物线L的“带线”,抛物线L叫做直线l的“路线”.
(a,b,c是常数,abc≠0)与直线l都经过y轴上的一点P,且抛物线L的顶点Q在直线l上,则称此直线l与该抛物线L具有“一带一路”关系.此时,直线l叫做抛物线L的“带线”,抛物线L叫做直线l的“路线”.
(1)若直线y=mx+1与抛物线![]() 具有“一带一路”关系,求m,n的值;
具有“一带一路”关系,求m,n的值;
(2)若某“路线”L的顶点在反比例函数![]() 的图象上,它的“带线”l的解析式为y=2x﹣4,求此“路线”L的解析式;
的图象上,它的“带线”l的解析式为y=2x﹣4,求此“路线”L的解析式;
(3)当常数k满足![]() ≤k≤2时,求抛物线L:
≤k≤2时,求抛物线L:![]() 的“带线”l与x轴,y轴所围成的三角形面积的取值范围.
的“带线”l与x轴,y轴所围成的三角形面积的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店尝试用单价随天数而变化的销售模式销售一种商品,利用30天的时间销售一种成本为10元/件的商品售后,经过统计得到此商品单价在第x天(x为正整数)销售的相关信息,如表所示:

(1)请计算第几天该商品单价为25元/件?
(2)求网店销售该商品30天里所获利润y(元)关于x(天)的函数关系式;
(3)这30天中第几天获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料:
∵ ![]() ;
; ![]() ;
; ![]() ;
;
… ![]()
∴ ![]()
= ![]()
= ![]()
= ![]()
解答下列问题:
(1)在和式 ![]() 中,第5项为 , 第n项为
中,第5项为 , 第n项为 ![]() ,上述求和的想法是:将和式中的各分数转化为两个数之差,使得首末两项外的中间各项可以 , 从而达到求和目的.
,上述求和的想法是:将和式中的各分数转化为两个数之差,使得首末两项外的中间各项可以 , 从而达到求和目的.
(2)利用上述结论计算:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
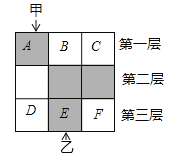
【题目】如图,3×3的方格分为上中下三层,第一层有一枚黑色方块甲,可在方格A、B、C中移动,第二层有两枚固定不动的黑色方块,第三层有一枚黑色方块乙,可在方格D、E、F中移动,甲、乙移入方格后,四枚黑色方块构成各种拼图.
(1)若乙固定在E处,移动甲后黑色方块构成的拼图是轴对称图形的概率是 .
(2)若甲、乙均可在本层移动.
①用树形图或列表法求出黑色方块所构拼图是轴对称图形的概率.
②黑色方块所构拼图是中心对称图形的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列顺序排列的等式:9 ![]() 0+1=1,9
0+1=1,9 ![]() 1+2=11,9
1+2=11,9 ![]() 2+3=21,9
2+3=21,9 ![]() 3+4=31,9
3+4=31,9 ![]() +5=41,……
+5=41,……
根据以上所反映的规律,猜想,第n个等式(n为正整数)应为( )
A.9(n-1)+n=10(n-1)+1
B.9n+n=(n-1)+n
C.9n+(n-1)=n2 -1
D.9n+n=10n+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过矩形ABCD的对角线BD上一点K分别作矩形两边的平行线MN与PQ,那么图中矩形AMKP的面积S1与矩形QCNK的面积S2的大小关系是;(填“>”或“<”或“=”) 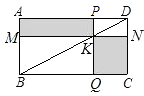
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com