
【题目】若抛物线L:![]() (a,b,c是常数,abc≠0)与直线l都经过y轴上的一点P,且抛物线L的顶点Q在直线l上,则称此直线l与该抛物线L具有“一带一路”关系.此时,直线l叫做抛物线L的“带线”,抛物线L叫做直线l的“路线”.
(a,b,c是常数,abc≠0)与直线l都经过y轴上的一点P,且抛物线L的顶点Q在直线l上,则称此直线l与该抛物线L具有“一带一路”关系.此时,直线l叫做抛物线L的“带线”,抛物线L叫做直线l的“路线”.
(1)若直线y=mx+1与抛物线![]() 具有“一带一路”关系,求m,n的值;
具有“一带一路”关系,求m,n的值;
(2)若某“路线”L的顶点在反比例函数![]() 的图象上,它的“带线”l的解析式为y=2x﹣4,求此“路线”L的解析式;
的图象上,它的“带线”l的解析式为y=2x﹣4,求此“路线”L的解析式;
(3)当常数k满足![]() ≤k≤2时,求抛物线L:
≤k≤2时,求抛物线L:![]() 的“带线”l与x轴,y轴所围成的三角形面积的取值范围.
的“带线”l与x轴,y轴所围成的三角形面积的取值范围.
【答案】(1)m=﹣1,n=1;(2)![]() 或
或![]() ;(3)
;(3)![]() ≤S≤
≤S≤![]() .
.
【解析】
试题分析:(1)找出直线y=mx+1与y轴的交点坐标,将其代入抛物线解析式中即可求出n的值;再根据抛物线的解析式找出顶点坐标,将其代入直线解析式中即可得出结论;
(2)找出直线与反比例函数图象的交点坐标,由此设出抛物线的解析式,再由直线的解析式找出直线与x轴的交点坐标,将其代入抛物线解析式中即可得出结论;
(3)由抛物线解析式找出抛物线与y轴的交点坐标,再根据抛物线的解析式找出其顶点坐标,由两点坐标结合待定系数法即可得出与该抛物线对应的“带线”l的解析式,找出该直线与x、y轴的交点坐标,结合三角形的面积找出面积S关于k的关系上,由二次函数的性质即可得出结论.
试题解析:(1)令直线y=mx+1中x=0,则y=1,即直线与y轴的交点为(0,1);
将(0,1)代入抛物线![]() 中,得n=1.
中,得n=1.
∵抛物线的解析式为![]() =
=![]() ,∴抛物线的顶点坐标为(1,0).
,∴抛物线的顶点坐标为(1,0).
将点(1,0)代入到直线y=mx+1中,得:0=m+1,解得:m=﹣1.
答:m=﹣1,n=1.
(2)将y=2x﹣4代入到![]() 中有,2x﹣4=
中有,2x﹣4=![]() ,即
,即![]() ,解得:
,解得:![]() ,
,![]() ,∴该“路线”L的顶点坐标为(﹣1,﹣6)或(3,2).
,∴该“路线”L的顶点坐标为(﹣1,﹣6)或(3,2).
令“带线”l:y=2x﹣4中x=0,则y=﹣4,∴“路线”L的图象过点(0,﹣4).
设该“路线”L的解析式为![]() 或
或![]() ,由题意得:
,由题意得:![]() 或
或![]() ,解得:m=2,n=
,解得:m=2,n=![]() ,∴此“路线”L的解析式为
,∴此“路线”L的解析式为![]() 或
或![]() .
.
(3)令抛物线L:![]() 中x=0,则y=k,即该抛物线与y轴的交点为(0,k).
中x=0,则y=k,即该抛物线与y轴的交点为(0,k).
抛物线L:![]() 的顶点坐标为(
的顶点坐标为(![]() ,
,![]() ),设“带线”l的解析式为y=px+k,∵点(
),设“带线”l的解析式为y=px+k,∵点(![]() ,
,![]() )在y=px+k上,∴
)在y=px+k上,∴![]() ,解得:p=
,解得:p=![]() ,∴“带线”l的解析式为
,∴“带线”l的解析式为![]() .
.
令∴“带线”l:![]() 中y=0,则
中y=0,则![]() ,解得:x=
,解得:x=![]() .
.
即“带线”l与x轴的交点为(![]() ,0),与y轴的交点为(0,k),∴“带线”l与x轴,y轴所围成的三角形面积S=
,0),与y轴的交点为(0,k),∴“带线”l与x轴,y轴所围成的三角形面积S=![]() =
=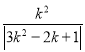 =
=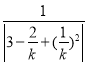 =
=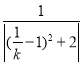 =
=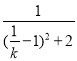 ,∵
,∵![]() ≤k≤2,∴
≤k≤2,∴![]() ≤
≤![]() ≤2,∴S=
≤2,∴S=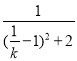 ,当
,当![]() =1时,S有最大值,最大值为
=1时,S有最大值,最大值为![]() ;当
;当![]() =2时,S有最小值,最小值为
=2时,S有最小值,最小值为![]() .
.
故抛物线L:y=ax2+(3k2﹣2k+1)x+k的“带线”l与x轴,y轴所围成的三角形面积的取值范围为![]() ≤S≤
≤S≤![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】以下问题,不适合用全面调查的是( )
A. 了解全班同学每周体育锻炼的时间
B. 调查七年级(1)班学生的某次数学考试成绩
C. 调查某班学生的身高
D. 了解全市中小学生每天的零花钱
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知命题:如图,点A,D,B,E在同一条直线上,且AD=BE,∠A=∠FDE,则△ABC≌△DEF.判断这个命题是真命题还是假命题,如果是真命题,请给出证明;如果是假命题,请添加一个适当条件使它成为真命题,并加以证明. 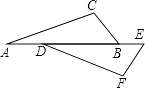
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,由若干个完全相同的小正方体堆成的一个几何体放置在平整的地面上.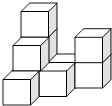
(1)请画出这个几何体的三视图.
(2)如果在这个几何体的表面喷上红色的漆,则在所有的小正方体中,有个小正方体只有一个面是红色,有个小正方体只有两个面是红色,有个小正方体只有三个面是红色.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设计一张折叠型方桌子如图,若AO=BO=50cm,CO=DO=30cm,将桌子放平后,要使AB距离地面的高为40cm,则两条桌腿需要叉开的∠AOB应为( ) 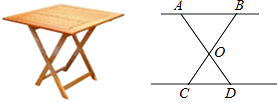
A.60°
B.90°
C.120°
D.150°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c图象上部分点的坐标满足下表:
x | … | -3 | -2 | -1 | 0 | 1 | … |
y | … | -3 | -2 | -3 | -6 | -11 | … |
则该函数图象上的点(﹣6,y1),(m2+2m+3,y2)则下列选项正确的是( )
A.y1>y2B.y1≥y2C.y1<y2D.y1≤y2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,以AC为一边向外作等边三角形ACD,点E为AB的中点,连结DE. 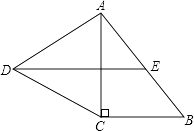
(1)证明DE∥CB;
(2)探索AC与AB满足怎样的数量关系时,四边形DCBE是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司计划从甲、乙两种产品中选择一种生产并销售,每年产销x件.已知产销两种产品的有关信息如表:

其中a为常数,且3≤a≤5.
(1)若产销甲、乙两种产品的年利润分别为![]() 万元、
万元、![]() 万元,直接写出
万元,直接写出![]() 、
、![]() 与x的函数关系式;
与x的函数关系式;
(2)分别求出产销两种产品的最大年利润;
(3)为获得最大年利润,该公司应该选择产销哪种产品?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com