
【题目】已知命题:如图,点A,D,B,E在同一条直线上,且AD=BE,∠A=∠FDE,则△ABC≌△DEF.判断这个命题是真命题还是假命题,如果是真命题,请给出证明;如果是假命题,请添加一个适当条件使它成为真命题,并加以证明. 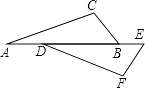
【答案】解:是假命题.
以下任一方法均可:
①添加条件:AC=DF.
证明:∵AD=BE,
∴AD+BD=BE+BD,即AB=DE.
在△ABC和△DEF中,
AB=DE,
∠A=∠FDE,
AC=DF,
∴△ABC≌△DEF(SAS);
②添加条件:∠CBA=∠E.
证明:∵AD=BE,
∴AD+BD=BE+BD,即AB=DE.
在△ABC和△DEF中,
∠A=∠FDE,
AB=DE,
∠CBA=∠E,
∴△ABC≌△DEF(ASA);
③添加条件:∠C=∠F.
证明:∵AD=BE,
∴AD+BD=BE+BD,即AB=DE.
在△ABC和△DEF中,
∠A=∠FDE,
∠C=∠F,
AB=DE,
∴△ABC≌△DEF(AAS)
【解析】本题中要证△ABC≌△DEF,已知的条件有一组对应边AB=DE(AD=BE),一组对应角∠A=∠FDE.要想证得全等,根据全等三角形的判定,缺少的条件是一组对应角(AAS或ASA),或者是一组对应边AC=EF(SAS).只要有这两种情况就能证得三角形全等.


科目:初中数学 来源: 题型:
【题目】阅读与应用:阅读1:a、b为实数,且a>0,b>0,因为![]() ,所以
,所以![]() 从而
从而![]() (当a=b时取等号).
(当a=b时取等号).
阅读2:若函数![]() ;(m>0,x>0,m为常数),由阅读1结论可知:
;(m>0,x>0,m为常数),由阅读1结论可知:![]() ,所以当
,所以当![]() ,即
,即![]() 时,函数
时,函数![]() 的最小值为
的最小值为![]() .
.
阅读理解上述内容,解答下列问题:
问题1:已知一个矩形的面积为4,其中一边长为x,则另一边长为![]() ,周长为2(
,周长为2(![]() ),求当x= 时,周长的最小值为 ;
),求当x= 时,周长的最小值为 ;
问题2:已知函数![]() (
(![]() )与函数
)与函数![]() (
(![]() ),
),
当x= 时,![]() 的最小值为 ;
的最小值为 ;
问题3:某民办学校每天的支出总费用包含以下三个部分:一是教职工工资4900元;二是学生生活费成本每人10元;三是其他费用.其中,其他费用与学生人数的平方成正比,比例系数为0.01.当学校学生人数为多少时,该校每天生均投入最低?最低费用是多少元?(生均投入=支出总费用÷学生人数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲经销商库存有1200套A品牌服装,每套进价400元,每套售价500元,一年内可卖完,现市场流行B品牌服装,每套进价300元,每套售价600元,但一年内只允许经销商一次性订购B品牌服装,一年内B品牌服装销售无积压,因甲经销商无流动资金可用,只有低价转让A品牌服装,用转让来的资金购进B品牌服装,并销售,经与乙经销商协商,甲、乙双方达成转让协议,转让价格y(元/套)与转让数量x(套)之间的函数关系式为![]() (
(![]() ),若甲经销商转让x套A品牌服装,一年内所获总利润为W(元).
),若甲经销商转让x套A品牌服装,一年内所获总利润为W(元).
(1)求转让后剩余的A品牌服装的销售款![]() (元)与x(套)之间的函数关系式;
(元)与x(套)之间的函数关系式;
(2)求B品牌服装的销售款![]() (元)与x(套)之间的函数关系式;
(元)与x(套)之间的函数关系式;
(3)求W(元)与x(套)之间的函数关系式,并求W的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD边长为3,点E在AB边上且BE=1,点P,Q分别是边BC,CD的动点(均不与顶点重合),当四边形AEPQ的周长取最小值时,四边形AEPQ的面积是 .
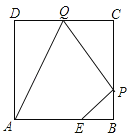
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线L:![]() (a,b,c是常数,abc≠0)与直线l都经过y轴上的一点P,且抛物线L的顶点Q在直线l上,则称此直线l与该抛物线L具有“一带一路”关系.此时,直线l叫做抛物线L的“带线”,抛物线L叫做直线l的“路线”.
(a,b,c是常数,abc≠0)与直线l都经过y轴上的一点P,且抛物线L的顶点Q在直线l上,则称此直线l与该抛物线L具有“一带一路”关系.此时,直线l叫做抛物线L的“带线”,抛物线L叫做直线l的“路线”.
(1)若直线y=mx+1与抛物线![]() 具有“一带一路”关系,求m,n的值;
具有“一带一路”关系,求m,n的值;
(2)若某“路线”L的顶点在反比例函数![]() 的图象上,它的“带线”l的解析式为y=2x﹣4,求此“路线”L的解析式;
的图象上,它的“带线”l的解析式为y=2x﹣4,求此“路线”L的解析式;
(3)当常数k满足![]() ≤k≤2时,求抛物线L:
≤k≤2时,求抛物线L:![]() 的“带线”l与x轴,y轴所围成的三角形面积的取值范围.
的“带线”l与x轴,y轴所围成的三角形面积的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com