
【题目】如图,将45°角三角板绕直角顶点旋转.
(1)问∠AOC与∠BOD大小关系,并说明理由;
(2)∠AOD与∠BOC的数量关系,并说明理由;
(3)若∠AOD=3∠BOC,求∠AOC的大小.
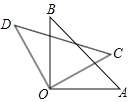
【答案】(1)∠AOC=∠BOD(2)∠AOD+∠BOC=180°;(3)45°.
【解析】
(1)由∠AOB-∠BOC=∠COD-∠BOC,即可得出结论;
(2)由角的关系容易得出结论;
(3)求出∠BOC=45°,即可得出∠AOC的度数.
(1)∠AOC=∠BOD;理由如下:
∵∠AOB=∠COD=90°,
∴∠AOB-∠BOC=∠COD-∠BOC,
即∠AOC=∠BOD;
(2)∠AOD+∠BOC=180°;理由如下:
∵∠AOB=∠COD=90°,
∴∠AOD+∠BOC=∠AOB+∠BOD+∠BOC=∠AOB+∠COD=90°+90°=180°;
(3)∵∠AOD=3∠BOC,∠AOD+∠BOC=180°,
∴∠BOC=45°,
∵∠AOB=90°,
∴∠AOC=45°.


科目:初中数学 来源: 题型:
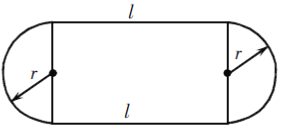
【题目】如图,操场的两端为半圆形,中间是一个长方形. 已知半圆的半径为r,直跑道的长为l,请用关于r,l的多项式表示这个操场的面积. 这个多项式能分解因式吗?若能,请把它分解因式,并计算当r=40m,l=30πm时操场的面积(结果保留π);若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题6分)在一次消防演习中,消防员架起一架25米长的云梯AB,如图斜靠在一面墙上,梯子底端B离墙角C的距离为7米。

(1)求这个梯子的顶端距地面的高度AC是多少?
(2)如果消防员接到命令,按要求将梯子底部在水平方向滑 动后停在DE的位置上(云梯长度不变),测得BD长为8米,那么云梯的顶部在下滑了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校八、九年级部分学生的睡眠情况,随机抽取了该校八、九年级部分学生进行调查,已知抽取的八年级与九年级的学生人数相同,利用抽样所得的数据绘制如图的统计图表:
睡眠情况分段情况如下
组别 | 睡眠时间x(小时) |
A | 4.5≤x<5.5 |
B | 5.5≤x<6.5 |
C | 6.5≤x<7.5 |
D | 7.5≤x<8.5 |
E | 8.5≤x<9.5 |
根据图表提供的信息,回答下列问题:
(Ⅰ)直接写出统计图中a的值 ![]()
(Ⅱ)睡眠时间少于6.5小时为严重睡眠不足,则从该校八、九年级各随机抽一名学生,被抽到的这两位学生睡眠严重不足的可能性分别有多大?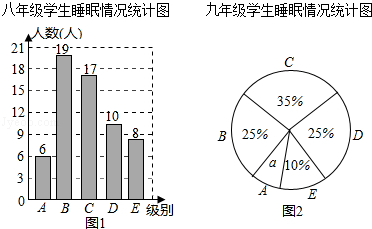
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合,研究数轴我们发现:若数轴上点A、点B表示的数分别为a、b,则A,B两点之间的距离AB=|a﹣b|,线段AB的中点表示的数为![]() .如:如图,数轴上点A表示的数为﹣2,点B表示的数为8,则A、两点间的距离AB=|﹣2﹣8|=10,线段AB的中点C表示的数为
.如:如图,数轴上点A表示的数为﹣2,点B表示的数为8,则A、两点间的距离AB=|﹣2﹣8|=10,线段AB的中点C表示的数为![]() =3,点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒2个单位长度的速度向左匀速运动.设运动时间为t秒(t>0).
=3,点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒2个单位长度的速度向左匀速运动.设运动时间为t秒(t>0).
(1)用含t的代数式表示:t秒后,点P表示的数为 ,点Q表示的数为 .
(2)求当t为何值时,P、Q两点相遇,并写出相遇点所表示的数;
(3)求当t为何值时,PQ=![]() AB;
AB;
(4)若点M为PA的中点,点N为PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请求出线段MN的长.
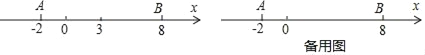
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地雪灾发生之后,灾区急需帐篷。某车间的甲、乙两名工人分别同时生产同种帐篷上的同种零件,他们一天生产零件y(个)与生产时间t(时)的函数关系如图所示。
①甲、乙中______先完成一天的生产任务;在生产过程中,______因机器故障停止生产______小时。
②当t=______时,甲、乙生产的零件个数相等。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,因为直线AB、CD相交于点P,AB∥EF,所以CD不平行于EF(________________________________________________________);
(2)因为直线a∥b,b∥c,所以a∥c(________________________________).
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习了二次根式的相关运算后,我们发现一些含有根号的式子可以表示成另一个式子的平方,如:
3+2![]() =2+2
=2+2![]() +1=(
+1=(![]() )2+2
)2+2![]() +1=(
+1=(![]() +1)2;
+1)2;
5+2![]() =2+2
=2+2![]() +3=(
+3=(![]() )2+2×
)2+2×![]() ×
×![]() +(
+(![]() )2=(
)2=(![]() +
+![]() )2
)2
(1)请仿照上面式子的变化过程,把下列各式化成另一个式子的平方的形式:
①4+2![]() ;②6+4
;②6+4![]()
(2)若a+4![]() =(m+n
=(m+n![]() )2,且a,m,n都是正整数,试求a的值.
)2,且a,m,n都是正整数,试求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列解题过程
已知a、b、c为△ABC为三边,且满足a2c2-b2c2=a4-b4,试判断△ABC的形状
解:∵a2c2-b2c2=a4-b4①
∴c2(a2-b2)=(a2-b2)(a2+b2)②
∴c2=a2+b2③
∴△ABC是直角三角形
回答下列问题:
(1)上述解题过程,从哪一步开始出现错误?请写出该步的序号________.
(2)错误原因为________.
(3)本题正确结论是什么,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com