
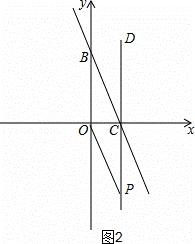
如图,直线y=﹣2x+4与坐标轴分别交于C、B两点,过点C作CD⊥x轴,点P是x轴下方直线CD上的一点,且△OCP与△OBC相似,求过点P的双曲线解析式.
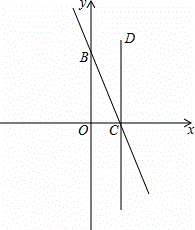
解:∵直线y=﹣2x+4与坐标轴分别交于C、B两点,
∴令y=0,可得﹣2x+4=0,解得x=2,即C(2,0),OC=2,
令x=0,可得y=4,即B(0,4),OB=4,
①如图1,当∠OBC=∠COP时,△OCP与△OBC相似,
∴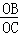 =
=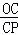 ,即
,即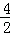 =
= ,解得CP=2,
,解得CP=2,
∴P(2,﹣1),
设过点P的双曲线解析式y=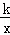 ,把P点代入得﹣1=
,把P点代入得﹣1=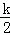 ,解得k=﹣2,
,解得k=﹣2,
∴过点P的双曲线解析式y= ,
,
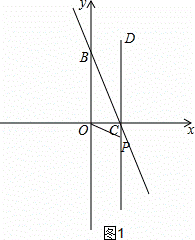
②如图2,当∠OBC=∠CPO时,△OCP与△OBC相似,
在△OCP和△COB中,
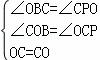
∴△OCP≌△COB(AAS)
∴CP=BO=4,
∴P(2,﹣4)
设过点P的双曲线解析式y=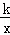 ,把P点代入得﹣4=
,把P点代入得﹣4=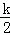 ,解得k=﹣8,
,解得k=﹣8,
∴过点P的双曲线解析式y=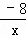 ,
,


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
如图 ,在△ABC中,点D是边AB上一点,点E是边AC上一点,且DE∥BC,∠B=40°,∠AED=60°,则∠A的度数是( )
,在△ABC中,点D是边AB上一点,点E是边AC上一点,且DE∥BC,∠B=40°,∠AED=60°,则∠A的度数是( )
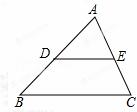
A.100° B.90° C.8 0° D.70°
0° D.70°
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在矩形ABCD中,AB=5,BC=7,点E为BC上一动点,把△ABE沿AE折叠,当点B的对应点B′落在∠ADC的角平分线上时,则点B′到BC的距离为( )

A.1或2 B. 2或3 C. 3或4 D. 4或5
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在△ABC中,∠C=90°,AC=BC,斜边AB=2,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,弧EH经过点C,则图中阴影部分的面积为 .
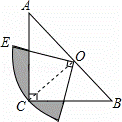
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com